2024XYCTF

Posted on | In |

记录上半年打的新生赛，一场记忆犹新的crypto入门赛

Crypto

Sign1n_Revenge

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
from Crypto.Util.number import *
from tqdm import *
import gmpy2
flag=b'XYCTF{uuid}'
flag=bytes_to_long(flag)
leak=bin(int(flag))
while 1:
    leak += "0"
    if len(leak) == 514:
        break

def swap_bits(input_str):
    input_list = list(input_str[2:])
    length = len(input_list)

    for i in range(length // 2):
        temp = input_list[i]
        input_list[i] = input_list[length - 1 - i]
        input_list[length - 1 - i] = temp

    return ''.join(input_list)

input_str = leak
result = swap_bits(input_str)
a=result

def custom_add(input_str):
    input_list = list(input_str)
    length = len(input_list)
    
    for i in range(length):
        input_list[i] = str((int(input_list[i]) + i + 1) % 10)

    result = ''.join(input_list)
    return result


input_str = a
result = custom_add(input_str)
b=result
print(b)
#12345678901234567890123456789012345678901234567890123456789012345678901234567890123456789012345678901234567890123456789012345678901234567890123456789012345678901234567890123456799123455679902334667900133557889013356679001344568990233467780112346788902234677990134456899023356779001335668890123566780113445778912234568900133566889113346779011344577990233457790013356688911334677991124557780122355678011335668890124566789112455689902335567801134557889113356678902344567801223566890113455689911234677891224556899023

​ crypto部分的签到题啦，简单分析一下题目的意思，首先是对几个函数进行分析，先把输出的结果加到514位，然后将每一位作一个加i加1再模10的操作，再将前两位去掉，将剩下的512位作倒置，然后输出

​ 这样的话，我们对其进行逆向的分析，就可以得到原先的二进制数，分析的代码如下所示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <iostream>
using namespace std;
int len = 512;
char c[512];
char ans[512];

int main() {
	for (int i = 0; i < 512; i++)
		cin >> c[i];
	for (int i = 0; i < 512; i++) {
		c[i] = char((int(c[i]) - '0' - i - 1 + 1000) % 10 + '0');
		ans[511 - i] = c[i];
	}
	for (int i = 0; i < 512; i++) {
		cout << ans[i];
	}
	return 0;
}

​ 然后解出我们的二进制代码，我们将后面的0都去掉，剩下前面的

1
11001100110110001100001011001110111101100111000001110000011010100110111011000010110011001100100001110000010110101100001001110010110010101100101001011010011010001100101001101110110010100101101001110000011000100110110001100000010110100110111011001100011000101100010001110000110011001100110001100110011010000110101001100100110010001111101

​ 我们还需要在前面补充两位的二进制数，再将其bytes_to_long即可

​ 经过尝试，我们补充两个0，最后获得了flag

1
flag{8857afd8-a9ee-4e7e-8160-7f1b8ff3452d}

Sign1n[签到]

​ 跟上面一题的思路是一样的，得到flag即可

1
flag{8857afd8-a9ee-4e7e-8160-7f1b8ff3452d}

happy_to_solve1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from Crypto.Util.number import *
import sympy
from secrets import flag


def get_happy_prime():
    p = getPrime(512)
    q = sympy.nextprime(p ^ ((1 << 512) - 1))
    return p, q


m = bytes_to_long(flag)
p, q = get_happy_prime()
n = p * q
e = 65537
print(n)
print(pow(m, e, n))
# 24852206647750545040640868093921252282805229864862413863025873203291042799096787789288461426555716785288286492530194901130042940279109598071958012303179823645151637759103558737126271435636657767272703908384802528366090871653024192321398785017073393201385586868836278447340624427705360349350604325533927890879
# 14767985399473111932544176852718061186100743117407141435994374261886396781040934632110608219482140465671269958180849886097491653105939368395716596413352563005027867546585191103214650790884720729601171517615620202183534021987618146862260558624458833387692782722514796407503120297235224234298891794056695442287

​ 这题主要是一个happyprime函数，生成两个512位的素数，有一定的联系，这题与之前做的一题几乎一模一样，直接套用脚本即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import gmpy2
import sympy
import libnum
n = 24852206647750545040640868093921252282805229864862413863025873203291042799096787789288461426555716785288286492530194901130042940279109598071958012303179823645151637759103558737126271435636657767272703908384802528366090871653024192321398785017073393201385586868836278447340624427705360349350604325533927890879
c = 14767985399473111932544176852718061186100743117407141435994374261886396781040934632110608219482140465671269958180849886097491653105939368395716596413352563005027867546585191103214650790884720729601171517615620202183534021987618146862260558624458833387692782722514796407503120297235224234298891794056695442287
e = 65537
p=(gmpy2.iroot(pow(2,1024)-4*n,2)[0]+pow(2,512))//2
# p=(2**1024+gmpy2.iroot((2**1024)**2-4*n,2)[0])//2
p=int(p)
while(1):
    p=sympy.nextprime(p)
    if(n%p==0):
        print(p)
        break
q=n//p
phi=(p-1)*(q-1)
d=gmpy2.invert(e,phi)
m=pow(c,d,n)
flag=libnum.n2s(int(m))
print(flag)

​ 然后我们就可以得到flag

1
XYCTF{3f22f4efe3bbbc71bbcc999a0a622a1a23303cdc}

happy_to_solve2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import random
from Crypto.Util.number import *
from secrets import flag



def get_happy_prime():    while 1:
        p = int("".join([random.choice("123") for _ in range(512)]))
        q = int("".join([random.choice("567") for _ in range(512)]))
        if isPrime(p) and isPrime(q):
            return (p,q)

m = bytes_to_long(flag)
p ,q= get_happy_prime()
n = p * q
e = 65537
print(n)
print(pow(m, e, n))
# 697906506747097082736076931509594586899561519277373830451275402914416296858960649459482027106166486723487162428522597262774248272216088755005277069446993003521270487750989061229071167729138628583207229945902389632065500739730301375338674342457656803764567184544685006193130563116558641331897204457729877920989968662546183628637193220770495938729301979912328865798266631957128761871326655572836258178871966196973138373358029531478246243442559418904559585334351259080578222274926069834941166567112522869638854253933559832822899069320370733424453856240903784235604251466010104012061821038897933884352804297256364409157501116832788696434711523621632436970698827611375698724661553712549209133526623456888111161142213830821361143023186927163314212097199831985368310770663850851571934739809387798422381702174820982531508641022827776262236373967579266271031713520262606203067411268482553539580686495739014567368858613520107678565628269250835478345171330669316220473129104495659093134763261751546990704365966783697780787341963138501
# 153383826085102296581238539677668696644156148059026868813759015106139131297135097831661048493079405226972222492151356105759235749502324303047037349410709021152255315429280760639113724345836532087970918453353723090554450581657930847674930226113840172368662838756446364482977092478979838209396761279326533419699056209983721842484996150025403009644653678928025861445324715419893797015875541525590135843027312322236085581571452084477262582966972702577136904385741443870527205640874446616413917231260133364227248928492574610248881137364204914001412269740461851747883355414968499272944590071623223603501698004227753335552646715567802825755799597955409228004284739743749531270833084850113574712041224896044525292591264637452797151098802604186311724597450780520140413704697374209653369969451501627583467893160412780732575085846467289134920886789952338174193202234175299652687560232593212131693456966318670843605238958724126368185289703563591477049105538528244632434869965333722691837462591128379816582723367039674028619947057144546

​ 这题的两个素数较大，且不太能进行分解，于是我们观察生成两个素数的函数，发现第一个素数由123组成，第二个素数由567组成，于是想到根据乘积末尾部分来反推两个素数，由于存在多解性，我们利用dfs来求解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
m="697906506747097082736076931509594586899561519277373830451275402914416296858960649459482027106166486723487162428522597262774248272216088755005277069446993003521270487750989061229071167729138628583207229945902389632065500739730301375338674342457656803764567184544685006193130563116558641331897204457729877920989968662546183628637193220770495938729301979912328865798266631957128761871326655572836258178871966196973138373358029531478246243442559418904559585334351259080578222274926069834941166567112522869638854253933559832822899069320370733424453856240903784235604251466010104012061821038897933884352804297256364409157501116832788696434711523621632436970698827611375698724661553712549209133526623456888111161142213830821361143023186927163314212097199831985368310770663850851571934739809387798422381702174820982531508641022827776262236373967579266271031713520262606203067411268482553539580686495739014567368858613520107678565628269250835478345171330669316220473129104495659093134763261751546990704365966783697780787341963138501"
#temp1=3
#temp2=7
def dfs(i,temp1,temp2):
    flag=False
    if(str((int('1'+str(temp1)))*(int('5'+str(temp2))))[-i-1:]==(m[-i-1:])):
        t1=int('1'+str(temp1))
        t2=int('5'+str(temp2))
        i=i+1
        flag=True
        dfs(i,t1,t2)
        i=i-1
        
    if(str((int('1'+str(temp1)))*(int('6'+str(temp2))))[-i-1:]==(m[-i-1:])):
        t1=int('1'+str(temp1))
        t2=int('6'+str(temp2))
        i=i+1
        flag=True
        dfs(i,t1,t2)
        i=i-1      
  
    if(str((int('1'+str(temp1)))*(int('7'+str(temp2))))[-i-1:]==(m[-i-1:])):
        t1=int('1'+str(temp1))
        t2=int('7'+str(temp2))
        i=i+1
        flag=True
        dfs(i,t1,t2)
        i=i-1     
        
    if(str((int('2'+str(temp1)))*(int('5'+str(temp2))))[-i-1:]==(m[-i-1:])):
        t1=int('2'+str(temp1))
        t2=int('5'+str(temp2))
        i=i+1
        flag=True
        dfs(i,t1,t2)
        i=i-1                 
   
    if(str((int('2'+str(temp1)))*(int('6'+str(temp2))))[-i-1:]==(m[-i-1:])):
        t1=int('2'+str(temp1))
        t2=int('6'+str(temp2))
        i=i+1
        flag=True
        dfs(i,t1,t2)
        i=i-1                     
        
    if(str((int('2'+str(temp1)))*(int('7'+str(temp2))))[-i-1:]==(m[-i-1:])):
        t1=int('2'+str(temp1))
        t2=int('7'+str(temp2))
        i=i+1
        flag=True
        dfs(i,t1,t2)
        i=i-1                 
        
    if(str((int('3'+str(temp1)))*(int('5'+str(temp2))))[-i-1:]==(m[-i-1:])):
        t1=int('3'+str(temp1))
        t2=int('5'+str(temp2))
        i=i+1
        flag=True
        dfs(i,t1,t2)
        i=i-1
        
    if(str((int('3'+str(temp1)))*(int('6'+str(temp2))))[-i-1:]==(m[-i-1:])):
        t1=int('3'+str(temp1))
        t2=int('6'+str(temp2))
        i=i+1
        flag=True
        dfs(i,t1,t2)
        i=i-1
        
    if(str((int('3'+str(temp1)))*(int('7'+str(temp2))))[-i-1:]==(m[-i-1:])):
        t1=int('3'+str(temp1))
        t2=int('7'+str(temp2))
        i=i+1
        flag=True
        dfs(i,t1,t2)
        i=i-1
    if(i==512):
        print(temp1,temp2)
        return
    if(flag==False):
        return

dfs(1,3,7)

​ 求解出来由很多组解，我们再去对照前面的位数，最后获得了两个素数

​ 然后我们再使用RSA解密即可，求出逆元，求出d，在正向求解即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from gmpy2 import *
import libnum
import gmpy2
import random
from Crypto.Util.number import *


p=12121111312111223223122131311333233122132311113333112131132223222322113121112211311111122233111221112223111221331112322222333332331231122322123321123123133323213331321113332333332231113221231213322231322132311333132111221123111323112322131123322323331121233332123131222321123312221122323311122131121132332322222321213223131211322122311113331331222212121313131121212322112122212323321311231113213233312223111132133321123211122222213321223332322123131333322121223233122311222211311133331123122122331232313131221113
q=57577765666565565655657656576766776756666756575575655557577765666657666756565556567577677665557556655765767767655556677756576555657667566766667676566655656776775755756775755667657675665677575667656666776656677656575665766556767757667556655755567556776556675656666757767667757657665757566667776555777667667675756767666767666557555757566576666656676677575575577567765566577557756566766557765676756756557667655756575677676567766776665777656776577676577576757576665777555555575575656555655657776566765775556575765677
phi=(p-1)*(q-1)
e=65537
c=153383826085102296581238539677668696644156148059026868813759015106139131297135097831661048493079405226972222492151356105759235749502324303047037349410709021152255315429280760639113724345836532087970918453353723090554450581657930847674930226113840172368662838756446364482977092478979838209396761279326533419699056209983721842484996150025403009644653678928025861445324715419893797015875541525590135843027312322236085581571452084477262582966972702577136904385741443870527205640874446616413917231260133364227248928492574610248881137364204914001412269740461851747883355414968499272944590071623223603501698004227753335552646715567802825755799597955409228004284739743749531270833084850113574712041224896044525292591264637452797151098802604186311724597450780520140413704697374209653369969451501627583467893160412780732575085846467289134920886789952338174193202234175299652687560232593212131693456966318670843605238958724126368185289703563591477049105538528244632434869965333722691837462591128379816582723367039674028619947057144546
d=invert(e,phi)
n=697906506747097082736076931509594586899561519277373830451275402914416296858960649459482027106166486723487162428522597262774248272216088755005277069446993003521270487750989061229071167729138628583207229945902389632065500739730301375338674342457656803764567184544685006193130563116558641331897204457729877920989968662546183628637193220770495938729301979912328865798266631957128761871326655572836258178871966196973138373358029531478246243442559418904559585334351259080578222274926069834941166567112522869638854253933559832822899069320370733424453856240903784235604251466010104012061821038897933884352804297256364409157501116832788696434711523621632436970698827611375698724661553712549209133526623456888111161142213830821361143023186927163314212097199831985368310770663850851571934739809387798422381702174820982531508641022827776262236373967579266271031713520262606203067411268482553539580686495739014567368858613520107678565628269250835478345171330669316220473129104495659093134763261751546990704365966783697780787341963138501
m=pow(c,d,n)
print(m)
flag=long_to_bytes(m)
print(flag)

​ 解出flag

1
XYCTF{7f4b2241951976ce5ef6df44503209059997e5085d1bc21f6bef4d9effb29fd0}

happy_to_solve3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import gmpy2
from Crypto.Util.number import *
import random
from secrets import flag

n = 1024
rho = 2
gamma = 0.352
delta = (1 - gamma) / 2


def get_happy_prime():
    p = getPrime(n // 2)
    q = getPrime(n // 2)
    N = p * q
    if 2 * q - p > gmpy2.iroot(N, 3)[0] and 2 * q - p < int(N**gamma / 16):
        d = random.randint(int(N ** (delta - 0.001)), int(N**delta))
        e = gmpy2.invert(d, (p - 1) * (q - 1))
        return N, e


N, e = get_happy_prime()
m = bytes_to_long(flag)
print(N)
print(e)
print(pow(m, e, N))
# 262520792590557046276663232446026434827811478251833823563978322470880473096166170973396967071440576532100045206129176936699321058518888771220060450723297988984995658582283884954240129867538637146924315603797818982078845855992582229939200744016516540207525916858674450616913948112117516831530578235916528257187
# 202935305174706906986376186864051444100197589482194720650385604617995167023220940138899902073948844285283834058445151666398192104922822110762965750590312021079147170573038600118139119881722125346545331027913695559130179278058419339157557267195396326664433859683010193688491694572425231599139974726246205888139
# 66173406204647583141174847814283540389326401056490970592017577810775087017197392456634167609680060931553017712058528056769618111925816921272571306246667527546366331057781905353553621522209713637253380859235235590286779517552635935384231694255450099095196595516174794966487058693308544109311774074970769293357

论文题

我们还是使用我们的连分数攻击去完成，将下面的底换一下就可以了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
from Crypto.Util.number import *
N = 262520792590557046276663232446026434827811478251833823563978322470880473096166170973396967071440576532100045206129176936699321058518888771220060450723297988984995658582283884954240129867538637146924315603797818982078845855992582229939200744016516540207525916858674450616913948112117516831530578235916528257187
e = 202935305174706906986376186864051444100197589482194720650385604617995167023220940138899902073948844285283834058445151666398192104922822110762965750590312021079147170573038600118139119881722125346545331027913695559130179278058419339157557267195396326664433859683010193688491694572425231599139974726246205888139
c = 66173406204647583141174847814283540389326401056490970592017577810775087017197392456634167609680060931553017712058528056769618111925816921272571306246667527546366331057781905353553621522209713637253380859235235590286779517552635935384231694255450099095196595516174794966487058693308544109311774074970769293357
import mpmath

# numerator(n):分子, denominator(d)：分母
def t_cf(n, d):  # 将分数 x/y 转为连分数的形式
    res = []
    while d:
        res.append(n // d)
        n, d = d, n % d
    return res


def cf(sub_res):    # 得到渐进分数的分母和分子
    n, d = 1, 0
    for i in sub_res[::-1]:  # 从后面往前循环
        d, n = n, i * n + d
    return d, n
def list_fraction(x, y):     # 列出每个渐进分数
    res = t_cf(x, y)
    res = list(map(cf, (res[0:i] for i in range(1, len(res)))))  # 将连分数的结果逐一截取以求渐进分数
    return res

def wienerAttack(e, n):
    for (d, k) in list_fraction(e, n):  # 用一个for循环来注意试探e/n的连续函数的渐进分数，直到找到一个满足条件的渐进分数
        if k == 0:  # 可能会出现连分数的第一个为0的情况，排除
            continue
        if (e * d - 1) % k != 0:  # ed=1 (mod φ(n)) 因此如果找到了d的话，(ed-1)会整除φ(n),也就是存在k使得(e*d-1)//k=φ(n)
            continue

        phi = (e * d - 1) // k  # 这个结果就是 φ(n)
        
        print(phi)
        
mpmath.mp.dps = 100
n1 = N - int(mpmath.ceil(3 / mpmath.sqrt(2) * mpmath.sqrt(N))) + 1
cc = wienerAttack(e,n1)

得到结果：

1
2
3
4
202935305174706906986376186864051444100197589482194720650385604617995167023220940138899902073948844285283834058445151666398192104922822110762965750590312021079147170573038600118139119881722125346545331027913695559130179278058419339157557267195396326664433859683010193688491694572425231599139974726246205888138
262520564991961275420673875773070804282808796606754021607307335335619279893868790647768383959491270905218236399009898325893831488921437964561453566721084486842811658954058444408145925293802238746169279287173461489257763832041529698314457060542129716195693163164404676090644575106456469813355541773527006765933
262520792590557046276663232446026434827811478251833823563978322470880473096166170973396967071440576532100045206129176936699321058518888771220060450723297954614316778794257384313010822227390070404000045908427685570416864970143425964515572245710744222130111609693526759178286535258777660072393577806415536881976
262520792590557046276663232446026434827811478251833823563978322470880473096166170973396967071440576532100045206129176936699321058518888771220060450723297954614316778794257384313010822227390070404000045894108217119259056887931400362882611068288718174599033635822637538598755282646480225909171284360275954895012

然后我们再一一检验就可以了，找到第三个是符合条件的

1
2
3
4
5
6
7
8
N = 262520792590557046276663232446026434827811478251833823563978322470880473096166170973396967071440576532100045206129176936699321058518888771220060450723297988984995658582283884954240129867538637146924315603797818982078845855992582229939200744016516540207525916858674450616913948112117516831530578235916528257187
e = 202935305174706906986376186864051444100197589482194720650385604617995167023220940138899902073948844285283834058445151666398192104922822110762965750590312021079147170573038600118139119881722125346545331027913695559130179278058419339157557267195396326664433859683010193688491694572425231599139974726246205888139
c = 66173406204647583141174847814283540389326401056490970592017577810775087017197392456634167609680060931553017712058528056769618111925816921272571306246667527546366331057781905353553621522209713637253380859235235590286779517552635935384231694255450099095196595516174794966487058693308544109311774074970769293357
from gmpy2 import *
phi=262520792590557046276663232446026434827811478251833823563978322470880473096166170973396967071440576532100045206129176936699321058518888771220060450723297954614316778794257384313010822227390070404000045908427685570416864970143425964515572245710744222130111609693526759178286535258777660072393577806415536881976
d=invert(e,phi)
m=pow(c,d,N)
print(long_to_bytes(m))

输出我们的flag

1
XYCTF{68f1880cdafd99fbf9a156946cb39dd86477886f1d115636e149e12c16f99af0}

factor1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import gmpy2
import hashlib
from Crypto.Util.number import *

p = getPrime(512)
q = getPrime(512)
d = getPrime(512)
e = gmpy2.invert(d, (p**3 - 1) * (q**3 - 1))
flag = "XYCTF{" + hashlib.md5(str(p + q).encode()).hexdigest() + "}"
print(e)
print(p * q)
# 172005065945326769176157335849432320425605083524943730546805772515111751580759726759492349719668775270727323745284785341119685198468883978645793770975366048506237371435027612758232099414404389043740306443065413069994232238075194102578269859784981454218948784071599231415554297361219709787507633404217550013282713899284609273532223781487419770338416653260109238572639243087280632577902857385265070736208291583497988891353312351322545840742380550393294960815728021248513046077985900158814037534487146730483099151396746751774427787635287611736111679074330407715700153025952858666841328055071403960165321273972935204988906850585454805923440635864200149694398767776539993952528995717480620593326867245714074205285828967234591508039849777840636255379730281105670496110061909219669860172557450779495125345533232776767292561378244884362014224844319802810586344516400297830227894063759083198761120293919537342405893653545157892446163
# 99075185389443078008327214328328747792385153883836599753096971412377366865826254033534293886034828804219037466246175526347014045811852531994537520303063113985486063022444972761276531422538694915030159420989401280012025249129111871649831185047820236417385693285461420040134313833571949090757635806658958193793

​ 这道题刚开始一直在考虑求e的逆元那一步，感觉有点问题，后来我用了低指数加密破解

​ 简单来说就是将逆元后面的那一串式子看成n的3次，然后对e和n的三次做连分数攻击就可以了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import gmpy2
n=99075185389443078008327214328328747792385153883836599753096971412377366865826254033534293886034828804219037466246175526347014045811852531994537520303063113985486063022444972761276531422538694915030159420989401280012025249129111871649831185047820236417385693285461420040134313833571949090757635806658958193793
e=172005065945326769176157335849432320425605083524943730546805772515111751580759726759492349719668775270727323745284785341119685198468883978645793770975366048506237371435027612758232099414404389043740306443065413069994232238075194102578269859784981454218948784071599231415554297361219709787507633404217550013282713899284609273532223781487419770338416653260109238572639243087280632577902857385265070736208291583497988891353312351322545840742380550393294960815728021248513046077985900158814037534487146730483099151396746751774427787635287611736111679074330407715700153025952858666841328055071403960165321273972935204988906850585454805923440635864200149694398767776539993952528995717480620593326867245714074205285828967234591508039849777840636255379730281105670496110061909219669860172557450779495125345533232776767292561378244884362014224844319802810586344516400297830227894063759083198761120293919537342405893653545157892446163
n_3=n*n*n



# numerator(n):分子, denominator(d)：分母
def t_cf(n, d):  # 将分数 x/y 转为连分数的形式
    res = []
    while d:
        res.append(n // d)
        n, d = d, n % d
    return res


def cf(sub_res):    # 得到渐进分数的分母和分子
    n, d = 1, 0
    for i in sub_res[::-1]:  # 从后面往前循环
        d, n = n, i * n + d
    return d, n
def list_fraction(x, y):     # 列出每个渐进分数
    res = t_cf(x, y)
    res = list(map(cf, (res[0:i] for i in range(1, len(res)))))  # 将连分数的结果逐一截取以求渐进分数
    return res

def wienerAttack(e, n):
    for (d, k) in list_fraction(e, n):  # 用一个for循环来注意试探e/n的连续函数的渐进分数，直到找到一个满足条件的渐进分数
        if k == 0:  # 可能会出现连分数的第一个为0的情况，排除
            continue
        if (e * d - 1) % k != 0:  # ed=1 (mod φ(n)) 因此如果找到了d的话，(ed-1)会整除φ(n),也就是存在k使得(e*d-1)//k=φ(n)
            continue

        phi = (e * d - 1) // k  # 这个结果就是 φ(n)
        
        print(phi)
          
wienerAttack(e,n_3)

​ 连分数破解完之后，我们得到了很多组可能的结果，我们一组一组进行验证，最后求出p1，p2，q1，q2，然后就可以解出答案了

1
2
3
4
5
6
7
8
9
10
11
import gmpy2
import hashlib
from Crypto.Util.number import *

n=99075185389443078008327214328328747792385153883836599753096971412377366865826254033534293886034828804219037466246175526347014045811852531994537520303063113985486063022444972761276531422538694915030159420989401280012025249129111871649831185047820236417385693285461420040134313833571949090757635806658958193793
p1=10754959493573546439510276829300246769373124436128170955050379041986504869221750743052397622171703140881050431144683659643071578143360949942206693325622779
p2=9212046353930376594996890089494718736894378991991381248242532319628627449681664076081705664941905594411935750003102856235503684466394327681725704255564467
q1=9212046353930376594996890089494718736894378991991381248242532319628627449681664076081705664941905594411935750003102856235503684466394327681725704255564467
q2=10754959493573546439510276829300246769373124436128170955050379041986504869221750743052397622171703140881050431144683659643071578143360949942206693325622779
flag = "XYCTF{" + hashlib.md5(str(p1 + q1).encode()).hexdigest() + "}"
print(flag)

​ 运行程序，得到flag

1
XYCTF{a83211a70e18145a59671c08ddc67ba4}

factor3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
from Crypto.Util.number import *
import random

flag = b'XYCTF{*****}'
m = bytes_to_long(flag)
def gainPrime():
    while True:
        x = random.getrandbits(256)
        y = random.getrandbits(256)

        if y % 2 == 0:
            continue

        p = x ** 3 + 3 * y ** 3
        if p.bit_length() == 768 and p % 2 == 1 and isPrime(p):
            return p

p, q = gainPrime(), gainPrime()
N = p * q
phi = (p ** 2 + p + 1) * (q ** 2 + q + 1)
d = getPrime(320)
e = inverse(d, phi)
c = d**2^m

print(f"N: {N}")
print(f"e: {e}")
print(f"c: {c}")

N: 913125842482770239379848062277162627509794409924607555622246822717218133091223291889541294440266178282194506242444509803611492259403578922020590849630191477864719052980160940803309686069818208833547621252544423652489179493083138385424424384165228024273745733240109761707533778691158938848158094054261174692601673435971526522219273943464877956131040249169850420336023942653021547841666224446678539579529590840999008107782784268926145671962239929431694391039559247
e: 494518390582436635999115147756676313570637682518235195828939117782099618734167908630788943568232122157772909140885391963441876427590731524706959546524212914108888799081844320513851526790475333924396837458796755678072486028072639014677580265244176441153444956871730684233063789931539669072735599696830757690822185323538738397827461580678488181113667710378657058297572328491762536595872579603698945272140918157163640403488075948987156585480146162739943419183496337465468187233821931312507662218106713861638334075899266373256620752680354704533272722692596941861606161634082613228896420520465402725359166156632884432690715903666803067996854084671477445131853993177110154928274312496230096270510089973592664248613332000290545537840595645944390047611474888693558676781309912289044962293014118087259307560444929227407113819165713213046898243995956550944640168932947118400215917515277554126694376415569909534496134700668701465649939
c: 4450931337369461482106945992542133557585962894030505065110870389112565329875502952762182372926117037373210509516570958483606566274369840551132381128665744266165792377925899683228751870742727716

​ 这题跟factor1是一样的，先是用wiener attack，再穷举求出d就可以了，再作异或操作即得到flag

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import gmpy2
n=913125842482770239379848062277162627509794409924607555622246822717218133091223291889541294440266178282194506242444509803611492259403578922020590849630191477864719052980160940803309686069818208833547621252544423652489179493083138385424424384165228024273745733240109761707533778691158938848158094054261174692601673435971526522219273943464877956131040249169850420336023942653021547841666224446678539579529590840999008107782784268926145671962239929431694391039559247
e=494518390582436635999115147756676313570637682518235195828939117782099618734167908630788943568232122157772909140885391963441876427590731524706959546524212914108888799081844320513851526790475333924396837458796755678072486028072639014677580265244176441153444956871730684233063789931539669072735599696830757690822185323538738397827461580678488181113667710378657058297572328491762536595872579603698945272140918157163640403488075948987156585480146162739943419183496337465468187233821931312507662218106713861638334075899266373256620752680354704533272722692596941861606161634082613228896420520465402725359166156632884432690715903666803067996854084671477445131853993177110154928274312496230096270510089973592664248613332000290545537840595645944390047611474888693558676781309912289044962293014118087259307560444929227407113819165713213046898243995956550944640168932947118400215917515277554126694376415569909534496134700668701465649939
n_2=n*n



# numerator(n):分子, denominator(d)：分母
def t_cf(n, d):  # 将分数 x/y 转为连分数的形式
    res = []
    while d:
        res.append(n // d)
        n, d = d, n % d
    return res


def cf(sub_res):    # 得到渐进分数的分母和分子
    n, d = 1, 0
    for i in sub_res[::-1]:  # 从后面往前循环
        d, n = n, i * n + d
    return d, n
def list_fraction(x, y):     # 列出每个渐进分数
    res = t_cf(x, y)
    res = list(map(cf, (res[0:i] for i in range(1, len(res)))))  # 将连分数的结果逐一截取以求渐进分数
    return res

def wienerAttack(e, n):
    for (d, k) in list_fraction(e, n):  # 用一个for循环来注意试探e/n的连续函数的渐进分数，直到找到一个满足条件的渐进分数
        if k == 0:  # 可能会出现连分数的第一个为0的情况，排除
            continue
        if (e * d - 1) % k != 0:  # ed=1 (mod φ(n)) 因此如果找到了d的话，(ed-1)会整除φ(n),也就是存在k使得(e*d-1)//k=φ(n)
            continue

        phi = (e * d - 1) // k  # 这个结果就是 φ(n)
        
        print(phi)
      
wienerAttack(e,n_2)

解出所有的可能

1
2
3
4
5
494518390582436635999115147756676313570637682518235195828939117782099618734167908630788943568232122157772909140885391963441876427590731524706959546524212914108888799081844320513851526790475333924396837458796755678072486028072639014677580265244176441153444956871730684233063789931539669072735599696830757690822185323538738397827461580678488181113667710378657058297572328491762536595872579603698945272140918157163640403488075948987156585480146162739943419183496337465468187233821931312507662218106713861638334075899266373256620752680354704533272722692596941861606161634082613228896420520465402725359166156632884432690715903666803067996854084671477445131853993177110154928274312496230096270510089973592664248613332000290545537840595645944390047611474888693558676781309912289044962293014118087259307560444929227407113819165713213046898243995956550944640168932947118400215917515277554126694376415569909534496134700668701465649938
989036781164873271998230295513352627141275365036470391657878235564199237468335817261577887136464244315545818281770783926883752855181463049413919093048425828217777598163688641027703053580950667848793674917593511356144972056145278029355160530488352882306889913743461368466127579863079338145471199393661515381644370647077476795654923161356976362227335420757314116595144656983525073191745159207397890544281836314327280806976151897974313170960292325479886838366992674930936374467643862625015324436213427723276668151798532746513241505360709409066545445385193883723212323268165226457792841040930805450718332313265768865381431807333606135993708169342954890263707986354220309856548624992460192541020179947185328497226664000581091075681191291888780095222949777387117353562619824578089924586028236174518615120889858454814227638331426426093796487991913101889280337865894236800431835030555108253388752831139819068992269401337402931299877
834499784107861823248506811839391279150451089249521892961334761257293106613908345814456342271391706141241784175244098938308166471559359447942994234759609292558749848450612290867124451458927125997419663211719525206747320172372578337268416697599547744446438364721045529643295145509473191560241324488401903603262437733471621046333841417394948805629314261263983785877153304329849280505534978081241970146737799390213643180886128163915826737997746649623654519872150069472977565957074509089856679993055079641514688753080012004870547520148098563899897719543757339391460397757514409823762709628285367099043592889317992480165583087437730177244691267883118188660003613486373386441462902337388287456485776830437620919534997750490295595106005152531158205344363874670380267068460476987763373869461324272250081508250818071249504569842141047016640786743176679719080285074348262300364360807030872588796760201274222339462227307378433723284272
833798804209868926885597743428680923994376689883858923648251158413609393250010581389051354245825579589148843110244363516749941829705615281705885230450674458287010099343692585025388132084483695633586838705373864316786817375599573951862278045946006150851323308670520946217691496264921675220721213447466068569831512505491584734807189423945368087744747402041988282527302954157122933011299755788279613894864647286144803716494106382662520738127669495201009984205649985714336107675613477358442423855011266706320679789186508955691828275482443228137631311692451634084140175322596818203008684232335802209167702814849777136786055309765737995819234264295466468414424886749653691547737803992981154373858670285950028806340656537153716451114378660962319338320775240176128965474201402381863526217391037528765336199252413877793657795095634278978406411712164357046958884719590893726787739613415378848305826544330558861623813812000519592914963
833798804209868926885597743428680923994376689883858923648251158413609393250010581389051354245825579589148843110244363516749941829705615281705885230450674458287010099343692585025388132084483695633586838705373864316786817375599573950104127077186395659995392757752995882899938289080362111941272988091485639339559843502059915205444870110902918436499616297599187963509517327010042875646498204271294817693848615863916356218338119052317606715052301065698671485777819689151877833072309866131554613724414897565192219044775533159747352618965075724249708246214305354069900520387953575676413961901660414173017690214722328166929435552701525033444467609524741628219332675647717566112424485499891287720591551300843895993070967137359177985875585111358639075519420435411163829529375854064770748125965898317391058461098059863041945954210826787800935108724310961342056565354878553782400682837769329116302566267706973304162817085732088023207009

​ 然后一个一个试，求出逆元d，d需要满足是320位二进制，即93位十进制

1
d=2109723047551375043305134722302342646596769444055829710618826161103186815230448177424794300667429

​ 然后就进行d的平方操作，再和c作异或就可以了，得到flag

1
XYCTF{I_love_to_read_the_crypto_paper_and_try_to_ak_them}

babyRSAMAX

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
from Crypto.Util.number import *
from gmpy2 import *
from random import choice

flag = b'XYCTF{******}'
e = '?'
def getBabyPrime(nbits):
    while True:
        p = 1
        while p.bit_length() <= nbits:
            p *= choice(sieve_base)
        
        if isPrime(p+1):
            return p+1

p = getBabyPrime(512)
q = getBabyPrime(512)
n = p*q
gift1 = (pow(p,e,n)-pow(q,e,n)) % n
gift2 = pow(p+q,e,n)

t = 65537
x = bytes_to_long(e)
y = pow(x, t, n)

m = bytes_to_long(flag)
c = powmod(m, e, n)

print(f'n = {n}')
print(f'gift1 = {gift1}')
print(f'gift2 = {gift2}')
print(f'c = {c}')
print(f'y = {y}')

'''
n = 39332423872740210783246069030855946244104982381157166843977599780233911183158560901377359925435092326653303964261550158658551518626014048783435245471536959844874036516931542444719549997971482644905523459407775392702211086149279473784796202020281909706723380472571862792003687423791576530085747716706475220532321
gift1 = 4549402444746338327349007235818187793950285105091726167573552412678416759694660166956782755631447271662108564084382098562999950228708300902201571583419116299932264478381197034402338481872937576172197202519770782458343606060544694608852844228400457232100904217062914047342663534138668490328400022651816597367310
gift2 = 111061215998959709920736448050860427855012026815376672067601244053580566359594802604251992986382187891022583247997994146019970445247509119719411310760491983876636264003942870756402328634092146799825005835867245563420135253048223898334460067523975023732153230791136870324302259127159852763634051238811969161011462
c = 16938927825234407267026017561045490265698491840814929432152839745035946118743714566623315033802681009017695526374397370343984360997903165842591414203197184946588470355728984912522040744691974819630118163976259246941579063687857994193309554129816268931672391946592680578681270693589911021465752454315629283033043
y = 1813650001270967709841306491297716908969425248888510985109381881270362755031385564927869313112540534780853966341044526856705589020295048473305762088786992446350060024881117741041260391405962817182674421715239197211274668450947666394594121764333794138308442124114744892164155894256326961605137479286082964520217

'''

​ 先是利用生成n的漏洞，破解出p和q

1
2
p=236438400477521597922950445153796265199072404577183190953114805170522875904551780358338769440558816351105253794964040981919231484098097671084895302287425479
q=166353789373057352195268575168397750362643822201253508941052835945420624983216456266478176579651490080696973849607356408696043718492499993062863415424578199

​ 然后我们就可以解出e了，利用求逆元的方式，求出e

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from gmpy2 import *
import libnum
import gmpy2
import random
from Crypto.Util.number import *
n=39332423872740210783246069030855946244104982381157166843977599780233911183158560901377359925435092326653303964261550158658551518626014048783435245471536959844874036516931542444719549997971482644905523459407775392702211086149279473784796202020281909706723380472571862792003687423791576530085747716706475220532321
p=236438400477521597922950445153796265199072404577183190953114805170522875904551780358338769440558816351105253794964040981919231484098097671084895302287425479
q=166353789373057352195268575168397750362643822201253508941052835945420624983216456266478176579651490080696973849607356408696043718492499993062863415424578199
c=1813650001270967709841306491297716908969425248888510985109381881270362755031385564927869313112540534780853966341044526856705589020295048473305762088786992446350060024881117741041260391405962817182674421715239197211274668450947666394594121764333794138308442124114744892164155894256326961605137479286082964520217
phi=(p-1)*(q-1)
e=65537
d=invert(e,phi)
m=powmod(c,d,n)
print(m)
print(long_to_bytes(m))
print(phi)

求解出

1
b'XYCTF{e==4096}'

​ 说明我们已经求解出了e的值为4096

​ 然后再进一步，但是我们发现，下一个mod似乎没有整数解，因为e和phi不互素（具体参考e与phi不互素的情况_e和phi不互素-CSDN博客）

​ 我们使用有限域上的解的方式，用sage环境分别解出p和q的有限域，然后再用CRT把两个解合起来，查找是否存在字符XYCTF即可

1
2
[(236438400477521597922950445153796265199072404577183190953114805170522875904551780358338769404214275971858584747720119200208117068403781208566503489403215434, 1), (36344540379246669047243921781711114415694316462518391812884210045, 1)]
[(166353789373057352195268575168397750362643822201253508941052835945420624983216456266478176543306949701450304802363434626984929302798183530544471602540368154, 1), (36344540379246669047243921781711114415694316462518391812884210045, 1)]

代码：

1
2
3
4
5
6
7
8
9
10
res1=[(236438400477521597922950445153796265199072404577183190953114805170522875904551780358338769404214275971858584747720119200208117068403781208566503489403215434, 1), (36344540379246669047243921781711114415694316462518391812884210045, 1)]
res2=[(166353789373057352195268575168397750362643822201253508941052835945420624983216456266478176543306949701450304802363434626984929302798183530544471602540368154, 1), (36344540379246669047243921781711114415694316462518391812884210045, 1)]

#循环使用中国剩余定理
for i in res1:
    for j in res2:
        m = libnum.solve_crt([int(i[0]),int(j[0])],[p,q])
        flag = long_to_bytes(m)
        if b'XYCTF' in flag:
            print(flag)

输出结果

1
XYCTF{Rabin_is_so_biggggg!}

Complex_dlp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
from Crypto.Util.number import *
from secrets import flag


class Complex:
    def __init__(self, re, im):
        self.re = re
        self.im = im

    def __mul__(self, c):
        re_ = self.re * c.re - self.im * c.im
        im_ = self.re * c.im + self.im * c.re
        return Complex(re_, im_)

    def __str__(self):
        if self.im == 0:
            return str(self.re)
        elif self.re == 0:
            if abs(self.im) == 1:
                return f"{'-' if self.im < 0 else ''}i"
            else:
                return f"{self.im}i"
        else:
            return f"{self.re} {'+' if self.im > 0 else '-'} {abs(self.im)}i"


def complex_pow(c, exp, n):
    result = Complex(1, 0)
    while exp > 0:
        if exp & 1:
            result = result * c
            result.re = result.re % n
            result.im = result.im % n
        c = c * c
        c.re = c.re % n
        c.im = c.im % n
        exp >>= 1
    return result


flag = flag.strip(b"XYCTF{").strip(b"}")
p = 1127236854942215744482170859284245684922507818478439319428888584898927520579579027
g = Complex(3, 7)
x = bytes_to_long(flag)

print(complex_pow(g, x, p))
# 5699996596230726507553778181714315375600519769517892864468100565238657988087817 + 198037503897625840198829901785272602849546728822078622977599179234202360717671908i

​ 这道题根据hint，首先考虑将复数域转化成实数域，方法就是将两边同时乘上对应的共轭复数，这样两边就变成整数了

1
2
3
p =1127236854942215744482170859284245684922507818478439319428888584898927520579579027
g = 3**2 + 7**2
c=5699996596230726507553778181714315375600519769517892864468100565238657988087817**2+198037503897625840198829901785272602849546728822078622977599179234202360717671908**2

​ 然后就很简单了，用sage求一下离散对数，在转一下long_to_bytes就搞定了

求出flag是

1
XYCTF{___c0mp13x_d1p_15_3@5y_f0r_y0u___}

反方向的密码 相思

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from Crypto.Util.number import *
import hashlib
from secrets import flag


def hash(x):
    return hashlib.sha256(x.encode()).digest()


def pad(message):
    return message + hash(str(len(message)))


m = bytes_to_long(pad(flag))
p = getStrongPrime(512)
q = getStrongPrime(512)
n = p * q
e = 3   
print(pow(m, e, n))
print(n)
# 120440199294949712392334113337541924034371176306546446428347114627162894108760435789068328282135879182130546564535108930827440004987170619301799710272329673259390065147556073101312748104743572369383346039000998822862286001416166288971531241789864076857299162050026949096919395896174243383291126202796610039053
# 143413213355903851638663645270518081058249439863120739973910994223793329606595495141951165221740599158773181585002460087410975579141155680671886930801733174300593785562287068287654547100320094291092508723488470015821072834947151827362715749438612812148855627557719115676595686347541785037035334177162406305243

​ 这题的主要思路是，利用coppersmith来进行高低位的攻击，因为我们知道，flag的前几位必然是XYCTF{，所以相当于前面的m的位数已经知道了，包括最后的位数，也是可以确定的，所以我们就直接猜测flag的位数，然后逐一验证，看是否有正确的m。

​ 验算到38时终于出现了答案，说明flag的长度是38

​ 对应的m的值为58964190787951927773278389967057377362495121527440001979648729026891046689

​ 我们将其long_to_bytes即可，得到最后的flag

1
XYCTF{!__d3ng__hu0__1@n__3h@n__Chu__!}

fakeRSA

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
from Crypto.Util.number import *

flag = b'XYCTF{******}'
n = ZZ(bytes_to_long(flag))
p = getPrime(int(320))
print(p)

G = Zmod(p)

def function(X, Y, Z):
    def part(a, b, c):
        return vector([9 * a - 36 * c, 6 * a - 27 * c, b])
    def parts(n):
        Gx.<a, b, c> = G[]
        if n == 0: return vector([a, b, c])
        mid = parts(n // 2)
        result = mid(*mid)
        if n % 2 == 0: return result
        else: return part(*result)
    return parts(n)(X, Y, Z)

print(function(69, 48, 52))


#1849790472911267366045392456893126092698743308291512220657006129900961168811898822553602045875909
#(1431995965813617415860695748430644570118959991271395110995534704629241309597572003500157255135707, 1011565891130611736600822618382801465506651972373410962205810570075870804325974377971089090196019, 784497518859893244278116222363814433595961164446277297084989532659832474887622082585456138030246)

​ 这题是用jordan型正定矩阵来解决（根据hint）

​ 先尝试了一维的jordan矩阵，发现出不来，然后我们用n*n型来进行计算，将原jordan矩阵填充到3*3型

​ 我们先求出第二组和第三组解，根据前面的公式就可以得出来

1
2
3
b2 = vector(GF(p),[1431995965813617415860695748430644570118959991271395110995534704629241309597572003500157255135707,1011565891130611736600822618382801465506651972373410962205810570075870804325974377971089090196019,784497518859893244278116222363814433595961164446277297084989532659832474887622082585456138030246])
b1 = vector(GF(p), inv(b2))
b0 = vector(GF(p), inv(b1))

​ 在解出前三组解之后，我们就可以列出最后的表达式了

1
2
3
4
5
6
7
a = matrix(GF(p), [a0, a1, a2])
b = matrix(GF(p), [b0, b1, b2])
x = a.solve_right(b)
G = matrix(GF(p), [[9, 6, 0], [0, 0, 1], [-36, -27, 0]])
J, P = G.jordan_form(transformation=True)
H = ~P*x*P
long_to_bytes(int(3*H[0][1]/H[0][0])+3)

​ 这样就解出了最后的结果

1
XYCTF{y0u_finally_f0und_t3h_s3cr3ts!!}

x0r

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
import os

flag = open("flag.txt", "rb").read()
key = os.urandom(16)
iv = os.urandom(16)
flag = pad(flag, 16)


def aes_encrypt(key, plaintext):
    cipher = AES.new(key, AES.MODE_ECB)
    return cipher.encrypt(plaintext)


def encrypt(key, plaintext, iv):
    ciphertext = b""
    for i in range(0, len(plaintext), AES.block_size):
        key_block = aes_encrypt(key, iv)
        ciphertext_block = bytes(
            [plaintext[i + j] ^ key_block[j] for j in range(AES.block_size)]
        )
        ciphertext += ciphertext_block
        iv = key_block
    return ciphertext


while 1:
    try:
        print("1.print\n2.input\n3.exit")
        a = input("> ")
        if a == "1":
            print((iv + encrypt(key, flag, iv)).hex())
        elif a == "2":
            ivs = bytes.fromhex(input("iv: "))
            inputs = bytes.fromhex(input("message: "))
            print(encrypt(key, inputs, ivs).hex())
        elif a == "3":
            exit(0)
        else:
            print("You need input 1,2,3")
    except:exit(0)

​ 这题的话就是一个AES加密体制，AES加密的特点就是对称加密，就是说每次加密，明文都是一样的，所以我们可以通过明文去破解，输出的是128位密码，但是我们测试iv = os.urandom(16)发现生成的iv是32位的，所以我们将前32位当成iv输入，后面的96位当作message输入，这样就能解出公钥

image-20240414122313166

公钥是：58594354467b31663363626332312d663735362d346132382d613030372d6436653838633735653631667d0a04040404

​ 然后我们对其进行逆向解密即可，获得flag

1
XYCTF{1f3cbc21-f756-4a28-a007-d6e88c75e61f}

重生之我要当oi爷(未解决)

1
2
3
4
5
6
7
8
9
10
11
12
def f(a, b, p):
    t = 0
    for i in range(len(b)):
        t += pow(a, i, p) * b[i] % p
    return t % p

p = 1041231053

a = open("flag.png", "rb").read()
b = open("enc.txt", "w")
for i in range(len(a)):
    b.write(str(i) + str(f(i, a, p)) + "\n")

Complex_rsa

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
from Crypto.Util.number import *
from secrets import flag


class Complex:
    def __init__(self, re, im):
        self.re = re
        self.im = im

    def __mul__(self, c):
        re_ = self.re * c.re - self.im * c.im
        im_ = self.re * c.im + self.im * c.re
        return Complex(re_, im_)

    def __str__(self):
        if self.im == 0:
            return str(self.re)
        elif self.re == 0:
            if abs(self.im) == 1:
                return f"{'-' if self.im < 0 else ''}i"
            else:
                return f"{self.im}i"
        else:
            return f"{self.re} {'+' if self.im > 0 else '-'} {abs(self.im)}i"


def complex_pow(c, exp, n):
    result = Complex(1, 0)
    while exp > 0:
        if exp & 1:
            result = result * c
            result.re = result.re % n
            result.im = result.im % n
        c = c * c
        c.re = c.re % n
        c.im = c.im % n
        exp >>= 1
    return result


m = bytes_to_long(flag)
key = getRandomNBitInteger(m.bit_length())
c = m ^ key
com = Complex(key, c)
p = getPrime(512)
q = getPrime(512)
e = 9
enc = complex_pow(com, e, p * q)
print(enc)
print(Complex(p, q) * Complex(p, q))
# 66350931528185981323649477263900844564494528747802437244889229343520648562164950914433406604580038018765783183569276743239888668912948977370163046257917321742455772852779551569446155827368453262479370103326286297164105599131090881306108546341785251895116423206455175290083968296281375908109039893280371271943 + 65266730684129269806656018828265187384002656633231286337130178390517924611751697965395744944541329793503617856896706439809241745206839328124348693486741656130890593895436661857688522977866438805549144904296596887218275440542852887148071837153436265722614658566275517205322945316112048487893204059562830581004i
# -28814875173103880290298835537218644402443395484370652510062722255203946330565951328874411874019897676900075613671629765922970689802650462822117767927082712245512492082864958877932682404829188622269636302484189627580600076246836248427780151681898051243380477561480415972565859837597822263289141887833338111120 + 235362412848885579543400940934854106052672292040465052424316433330114813432317923674803623227280862945857543620663672974955235166884830751834386990766053503640556408758413592161122945636548462064584183165189050320898315823173824074873376450569212651128285746330837777597290934043912373820690250920839961482862i

首先就是根据我们给出的条件，将我们的p和q都计算出来，这个不难

然后根据我们在复数域上的欧拉函数，我们可以得到： 然后我们进行计算，但是发现我们的phi和e居然有公因数3，这样我们的逆元就不存在了

但是我们可以升次，通过升次去找到我们可能的解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
from Crypto.Util.number import *
from gmpy2 import *

e = 9
pq2 = 235362412848885579543400940934854106052672292040465052424316433330114813432317923674803623227280862945857543620663672974955235166884830751834386990766053503640556408758413592161122945636548462064584183165189050320898315823173824074873376450569212651128285746330837777597290934043912373820690250920839961482862
p2_q2 = -28814875173103880290298835537218644402443395484370652510062722255203946330565951328874411874019897676900075613671629765922970689802650462822117767927082712245512492082864958877932682404829188622269636302484189627580600076246836248427780151681898051243380477561480415972565859837597822263289141887833338111120

class Complex:
    def __init__(self, re, im):
        self.re = re
        self.im = im

    def __mul__(self, c):
        re_ = self.re * c.re - self.im * c.im
        im_ = self.re * c.im + self.im * c.re
        return Complex(re_, im_)

    def __str__(self):
        if self.im == 0:
            return str(self.re)
        elif self.re == 0:
            if abs(self.im) == 1:
                return f"{'-' if self.im < 0 else ''}i"
            else:
                return f"{self.im}i"
        else:
            return f"{self.re} {'+' if self.im > 0 else '-'} {abs(self.im)}i"


def complex_pow(c, exp, n):
    result = Complex(1, 0)
    while exp > 0:
        if exp & 1:
            result = result * c
            result.re = result.re % n
            result.im = result.im % n
        c = c * c
        c.re = c.re % n
        c.im = c.im % n
        exp >>= 1
    return result

p = 10205509456040823453782883291824829705816298450992336115902525676510986341532486274067943978039013674207011185602314114359146043975207543018267242312660911
q = pq2 // 2 // p

com = Complex(66350931528185981323649477263900844564494528747802437244889229343520648562164950914433406604580038018765783183569276743239888668912948977370163046257917321742455772852779551569446155827368453262479370103326286297164105599131090881306108546341785251895116423206455175290083968296281375908109039893280371271943 , 65266730684129269806656018828265187384002656633231286337130178390517924611751697965395744944541329793503617856896706439809241745206839328124348693486741656130890593895436661857688522977866438805549144904296596887218275440542852887148071837153436265722614658566275517205322945316112048487893204059562830581004)
re = int(complex_pow(com, inverse(3,(p^2-1)//3), p).re)
im = int(complex_pow(com, inverse(3,(p^2-1)//3), p).im)


PR.<a,b> = PolynomialRing(Zmod(p))
f1 = a^3 - 3*a*b^2 - re
f2 = 3*a^2*b - b^3 - im
h = f1.sylvester_matrix(f2, a).det()
res1 = h.univariate_polynomial().monic().roots()
print(res1)


re = int(complex_pow(com, inverse(3,(q^2-1)//3), q).re)
im = int(complex_pow(com, inverse(3,(q^2-1)//3), q).im)
PR.<a,b> = PolynomialRing(Zmod(q))
f1 = a^3 - 3*a*b^2 - re
f2 = 3*a^2*b - b^3 - im
h = f1.sylvester_matrix(f2, a).det()
res1 = h.univariate_polynomial().monic().roots()
print(res1)

这样就可以找出我们所有可能的解

然后用我们的CRT进行遍历，找出带flag头的就可以了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
from Crypto.Util.number import *
from sympy.ntheory.modular import crt
#M = crt(n,c)[0]

pq2 = 235362412848885579543400940934854106052672292040465052424316433330114813432317923674803623227280862945857543620663672974955235166884830751834386990766053503640556408758413592161122945636548462064584183165189050320898315823173824074873376450569212651128285746330837777597290934043912373820690250920839961482862
p2_q2 = -28814875173103880290298835537218644402443395484370652510062722255203946330565951328874411874019897676900075613671629765922970689802650462822117767927082712245512492082864958877932682404829188622269636302484189627580600076246836248427780151681898051243380477561480415972565859837597822263289141887833338111120
p = 10205509456040823453782883291824829705816298450992336115902525676510986341532486274067943978039013674207011185602314114359146043975207543018267242312660911
q = pq2 // 2 // p

resp = [(5741279734159523094711430662094390392066954482529914882030709450295074947781529110509321968864008611691202383770840412010325910906148313511187473860891035, 1), (4429927739780647098163182245695850111737474361073472216489514077452142827783532166774438977867801037416377640995299677179237078298139871084989841206362410, 1), (34301982100653260908270384034589202011869607388949017382302148763768565967424996784183031307204025099431160836174025169583054770919358422089927245407466, 1)]
resq = [(10739940731745824081418381715901342901309159762856543362640396906171107996295925365437945464907432967788383551341616951552057327658847904490010061152434332, 1), (8586549363626610854952590733794044071899545915261216635206863621255915665043556027382073545902963458915586846862230166123268280750109862724278599667847493, 1), (7045447028567292693464036821896048537001778022349939312880599967825498301190014724113928977446846014453607030578761699581827447107524459504793000974080961, 1), (5276901669007862459606429311418416791067007412160397323233728060764482838272522831695179159225558247215591099096136610833622276098301992005638773878483349, 1), (4073305908343434001432234700505703739500538013701467077531217640906529193773037971902079461771703238283853345951042314327641038705737553746426200870882295, 1), (3735799333948544298117875399520421256169239519249120000907464407334065474418981528427034590769440802753611282812668144292181442455716588786153175184716817, 1), (3722039472368511317694313824581779119019195065732852920938680419139949899687211960294412748248774573691326211744547172363931044270883035467641541946900209, 1), (2532203573284115839943680788607708204602770120790189755204953987476111829919496668633934893315585793821873529667573847786200205063152150526940602177115763, 1), (412391777749762922348152402206151838186656562632033608965544858648517072916178764607518361571369361991330463978453617074285039619075164749001716157536065, 1)]

cp = []
cq = []
for i in resp:
    cp.append(i[0])

for i in resq:
    cq.append(i[0])

KEY = []
for i in cp:
    for j in cq:
        n = [p,q]
        c = [i,j]
        key = crt(n,c)[0]
        KEY.append(key)


resp = [(8001885192071749859699066040025029961395167917875583646644249565155819105797467000967544636712092306411149367493633723366623965498649673837196063800580404, 1), (1662435559780994004386842122204566836802794060667449753807174598739830437128828179292947062605594949711892539092095892832053999186054026591407366803020136, 1), (541188704188079589696975129595232907618336472449302715451101512615336798606191093807452278721326418083969279016584498160468079290503842589663811709060371, 1)]
resq = [(8503432605028099223082740882529347146997316989367545950492333769305549393260049047195629451308480848275471020811688622917531588079409913760096873405190234, 1), (8366627759634051290333268012004602352405002740363136177900446298441200900164136168489014946546974693508397220434695162939560760156985163750847606373150919, 1), (7838336389145961788946008207588532360344213223957590603935032631402061939530140801549439038388256401440065798242555755132126684810445868962728928464941121, 1), (6857325280540966155209571629622673516628729233046153216919246004917826296064185951208599616644606134509118662339264343895819605897243323286865301166906602, 1), (6192229064658828721072838954681858729975625467636197870361944867014338842334277705562409203724381687673713439770131476110414702628279278489497356226657489, 1), (4121694029664041978927797165221546618939268589175297893513650941901521328887423207726634825943843128912526687991267349501555811582062174969259522939168771, 1), (2475586705176908911054627912314872988570680832853905159940563177513798231691560111739604991279968415146174329518843070479843829399895584496027950700885139, 1), (1217221620337618917243787804704498765774078541871944235501766658464684396657530547334482771121693798142550712746858805371783011221995724541464038836673061, 1), (552125404455481483107055129763683979120974776461988888944465520561196942927622301688292358201469351307145490177725937586378107953031679744096093896423948, 1)]
cp = []
cq = []
for i in resp:
    cp.append(i[0])

for i in resq:
    cq.append(i[0])

CC = []
for i in cp:
    for j in cq:
        n = [p,q]
        c = [i,j]
        cc = crt(n,c)[0]
        CC.append(cc)

for i in CC:
    for j in KEY:
        if(b"flag" in long_to_bytes(i ^ j)):
            print(long_to_bytes(i ^ j))
print(len(CC))

这样就得到了我们的flag

1
flag{Complex_is_so_fun_and_I_think_you_know_Sylvester!}

Random_rr(未解决)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from Crypto.Util.number import *

from random import randint
flag=b'XYCTF{uuid}'
flag = bytes_to_long(flag)
n = 472993274721871037103726599805149366727531552333249750035977291933239067588481589544777397613192273114354221827196579379954069925604091911249655707080927769808587176515295614018992848517984372306879552247519117116110554431341268358177159108949791969262793325836353834899335531293329721598226413212541536002401507477776699642647348576111445702197483449777741566350285229621935507081895389023444249054515395783080003733803406382744631528246608154546123270319561514117323480441428953306734274538511770278887429407127143049023747710881993279361892937905382946820141513009017756811296722630617325141162244806884220212939955235410280899112731530527048274396186038160728562551536558223235783656985493518204710943916486379681906506757757594165379493317173050550893487151879681122510523721157284728808336110950008840684602353984682117748018347433177541603140491131603068512706893984834735290809952944273565203183330739252949245209529232254867201402656024997949207918675051941911990640248052951780195402390132237903538546705181463959793972284823588987652138458328270662652334799233015314673544813649692428544375538627858921763941533600553536579901589575693816746953261108022490849251974419402753031545629158199093099096735356165044275617408697
rr = 11898141078345200236264081467585899457224809417108457314508072413792599039332439547789237898270544336909458761754683941320649771736625000667170176071314483
def generate():
    fw = open("random", "w")
    for i in range(648):
        fw.write(str(random.getrandbits(32))+"\n")
    fw.close()
generate()
key = str(random.getrandbits(32))
key1= int(str(key)[0])
ks = [randint(0, rr**(i+key1-1)) for i in range(16)]
c1 = pow(sum(k*flag**i for i, k in enumerate(ks)), 127, n)
c2 = pow(flag, 65537, n)
ks = [pow(69, k+key, rr**(i+key1)) for i, k in enumerate(ks)]
print(f"{ks = }")
print(f"{c1 = }")
print(f"{c2 = }")

反方向的密码 情难(未解决)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import hashlib
from Crypto.Util.number import *
from secrets import flag


def hash(x):
    return hashlib.sha512(x.encode()).digest() * 2


def pad(message):
    return (message[: len(message) // 2] + hash(str(len(message))) + message[len(message) // 2 :])


p = getStrongPrime(1024)
q = getStrongPrime(1024)
n = p * q
e = 2
m = bytes_to_long(pad(flag))
print(pow(m, e, n))
print(n)
# 3335299537518434350008670067273514020883265809787658909900831303201069228111667477512288715627313377374377192065531931991830331266940281529429758933125645068623703704431432931062515459304407129764836169638068667723468109909932687335727824459807903558617156661138991973933280805156893120951135488168923425258119689993859896540097318197048436676318334502053269738046279338047497258783747007084564814994803144049365117574904704816542523015746396519693505167963245600047742456478545640334467678554748227823020862550712083249012329745708139070338928730226897923885785783461594034339595106377701306570280371612953393097739
# 26278624299187148406559772770865336226934633734285979741424867540828670397865189685966828527168795621543490979182417570078991930822041468539855006585233692884235331084907340302530060261742100702658312435180527335101284800616106884692498603300926488358017928867672861988448488439356448543527810620591324774111321619391264173779312033252573140028630441135269056099074531502841259940379636699304810677716177080486265721322966814104627525953974143476452058638927511594884002185219080847495835727300670028011001853179659250270200020884333850083063514830095064730932997593930711871108436386821290545084229347398808220810263

easy_ecc

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
from Crypto.Util.number import *
from hashlib import sha256
from secret import flag, secret,SECRET

assert flag[6:-1] == sha256(long_to_bytes(secret)).hexdigest().encode()


class ECC_easy:
    def __init__(self):
        self.a = 1365855822212045061018261334821659180641576788523935479
        self.b = 17329427219955161804703200105884322768704934833367341
        self.p = 1365855822212045061018261334821659180641576788523935481

    def add(self, P, Q):
        mul_inv = lambda x: pow(x, -1, self.p)
        x1, y1 = P
        x2, y2 = Q
        if P!=Q:
            l=(y2-y1)*inverse(x2-x1,self.p)%self.p
        else:l=(3*x1**2+2*self.a*x1+1)*inverse(2*self.b*y1,self.p)%self.p
        temp1 = (self.b*l**2-self.a-x1-x2)%self.p
        temp2 = ((2*x1+x2+self.a)*l-self.b*l**3-y1)%self.p
        x3 = temp1
        y3 = temp2
        return x3, y3

    def mul(self, x, P):
        Q = SECRET
        x = x % self.p
        while x > 0:
            if x & 1:
                Q = self.add(Q, P)
            P = self.add(P, P)
            x >>= 1
        return Q

    def ispoint(self, x, y):
        return (self.a * x ** 2 + x ** 3+x) % self.p == (self.b * y ** 2) % self.p


ecc = ECC_easy()
LLLL = (1060114032187482137663886206406014543797784561116139791,752764811411303365258802649951280929945966659818544966)
assert ecc.ispoint(LLLL[0], LLLL[1])
END = ecc.mul(secret, LLLL)
print(END)

# (695174082657148306737473938393010922439779304870471540,414626357054958506867453055549756701310099524292082869)

​ 这题的话，我们首先将椭圆曲线转化成标准曲线，转化脚本在学习资料中已经给出。转完之后，我们尝试用hellman进行解密，发现报错，提示该点在奇异曲线上，于是我们选用奇异曲线的解密脚本来进行攻击，脚本如下所示。（实际上并不一定需要转化成标准曲线）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
A=1098066776930223927329092382214459309226361965213
B=1263248714105743124314734095577181018742053879965591734
p=1365855822212045061018261334821659180641576788523935481
LLLL = (804603363012007759329983017410816754946539644939,668360700828957783980888938878566241242911721895008218)
END=(933414165833077907509715600260551365988944141925739220,121346737700219338084994830488363509910434835223666824)

def attack(p, a2, a4, a6, Gx, Gy, Px, Py):
    """
    Solves the discrete logarithm problem on a singular curve (y^2 = x^3 + a2 * x^2 + a4 * x + a6).
    :param p: the prime of the curve base ring
    :param a2: the a2 parameter of the curve
    :param a4: the a4 parameter of the curve
    :param a6: the a6 parameter of the curve
    :param Gx: the base point x value
    :param Gy: the base point y value
    :param Px: the point multiplication result x value
    :param Py: the point multiplication result y value
    :return: l such that l * G == P
    """
    x = GF(p)["x"].gen()
    f = x ** 3 + a2 * x ** 2 + a4 * x + a6
    roots = f.roots()

    # Singular point is a cusp.
    if len(roots) == 1:
        alpha = roots[0][0]
        u = (Gx - alpha) / Gy
        v = (Px - alpha) / Py
        return int(v / u)

    # Singular point is a node.
    if len(roots) == 2:
        if roots[0][1] == 2:
            alpha = roots[0][0]
            beta = roots[1][0]
        elif roots[1][1] == 2:
            alpha = roots[1][0]
            beta = roots[0][0]
        else:
            raise ValueError("Expected root with multiplicity 2.")

        t = (alpha - beta).sqrt()
        u = (Gy + t * (Gx - alpha)) / (Gy - t * (Gx - alpha))
        v = (Py + t * (Px - alpha)) / (Py - t * (Px - alpha))
        return int(v.log(u))

    raise ValueError(f"Unexpected number of roots {len(roots)}.")


attack(p,0,A,B,804603363012007759329983017410816754946539644939,668360700828957783980888938878566241242911721895008218,933414165833077907509715600260551365988944141925739220,121346737700219338084994830488363509910434835223666824)

​ 使用sage，这样就解出了我们的sercet值，再带回到原式中，获得最后的flag

1
XYCTF{ec9a6e17537e81b7f593f65f7e2ca5d575e6b34c504c24e4afb40c1e9dc4be0d}

LCG_and_HNP(未解决)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
from Crypto.Util.number import *
import random
from secrets import flag


class LCG:
    def __init__(self, seed, a, b, p):
        self.seed = seed
        self.a = a
        self.b = b
        self.p = p

    def next(self):
        self.seed = (self.seed * self.a + self.b) % self.p
        return self.seed >> (self.p.bit_length() - 8)


m = bytes_to_long(flag)
p = getPrime(128)
a = random.randint(1, p)
b = random.randint(1, p)
seed = random.randint(1, p)
out = []
lcg = LCG(seed, a, b, p)
for i in range(30):
    out.append(lcg.next())
key = ""
while 1:
    key += str(lcg.next())
    if int(key) >= m:
        break

with open("out.txt", "w") as f:
    f.write(f"p={p}\n")
    f.write(f"a={a}\n")
    f.write(f"b={b}\n")
    f.write(f"out={out}\n")
    f.write(f"c={int(key)^m}")

铜匠

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
from Crypto.Util.number import *
from secrets import flag

m = bytes_to_long(flag)
m1 = getRandomRange(1, m)
m2 = getRandomRange(1, m)
m3 = m - m1 - m2


def task1():
    e = 149
    p = getPrime(512)
    q = getPrime(512)
    n = p * q
    d = inverse(e,(p-1)*(q-1))
    return (pow(m1, e, n), d >> 222 << 222, n)


def task2():
    e = 65537
    p = getPrime(1024)
    q = getPrime(1024)
    n = p * q
    return (pow(m2, e, n), (p + q) & ((1 << 624) - 1), n)


def task3():
    e = 65537
    p = getPrime(512)
    q = getPrime(512)
    n = p * q
    return (pow(m3, e, n), (p ^ q) >> 200, n)


c1, leak1, n1 = task1()
c2, leak2, n2 = task2()
c3, leak3, n3 = task3()
print(c1, leak1, n1)
print(c2, leak2, n2)
print(c3, leak3, n3)
# (89623543982221289730635223555830551523170205418976759060541832483843039074358160566735322009158596405712449020903311144480669706226166537602750967447480664875090686428406188847601970724994074417752345460791736191511081890913041143570455636020205647345764692062144226011846336769477026234106683791286490222089, 138474880017294332349992670187778287774153347391371789199005713563195654993662610111557185709277805165708109047494971468100563949333712521647405765501704478862377527360106399421209690341743821320754482338590671565510629203215009008479290995785318405211007685664887994061938667418220613430135743123498167435264, 146331610798417415036517077006943013321623040860385791423062775325646472298267580898028515394910588437521335092742913111680737790430660749825981979147191282007208147041227246620008377726207734522466015971515317594545750944838673018946440525615131606652748549901880641896940968837669894325535750125282351577689)
# (5473961166821344576614003060897848014482672788904094340704447882490091115468180944569409159343222459801235179587721232166576530621751748850763430788036935832653535110975154800191323351333883661451331971042214143454441651165718504131976920077768864850035471790911190772583977173388975105970866592974077361193822302653046511418190410043729876062517148438923211673300268277037622337403526399584759202097925983596261279676101079771530118525540842499517622478819211528345668513680064744443628779623340175578509413636950545134641050948185944279029949957748464529075830770617236599864271566534714755373562527112224962839980,62964793504732923650344975634773688108135580826064134090114181449607062497690184718845295432644650580930430061411603385577783897575232298084007041511817031640186953023971498914096209984730,20748652069632848434897928314437138341436264859802586939154590237186029244907936870477844563166827587536149170710720365760129683024401957095447466056746469055173897234659911291443605912459271248059341147358511860537769587963189092648473894868209838600346115919726589891777340166174017389513260737891557712152871714337946675533597049874155202056200170954033849176655928144354665553271709442011723088448485570394208728775665739819536229908847043007472178803394055783543378990699834066614262050119443421709878598533329555838915158259138297060574425019923291353077080236769586821808150397875920110335669136563171420068201)
# (34640310217688693418173336791306022698488916505988760907493665070072623574363578354500529023855888624978101429772253437880445815006839767802433777006836665709335479076676231470534690281412388704665083311568028710188940132495410474044569100181764053297307413009214044407982980600917158732129850605715306726034, 3763587651775261955566046684899146246387485307521708557610018711932791630073528010801142052497, 94848869174430082173244966077736519396702141299429965725051314270443078621842166791082354594193554380275167898342497998871366256044865879909218309960595691008663632410356093966762639308253848450178310347612630814852054763933063313537694449475061227647475480417779126252294793767003555255527593551612032661749)

这题就是一个coppersmith练习，只不过第一个形式貌似是对d的高位攻击，平时没有怎么见过

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
from Crypto.Util.number import *
from tqdm import *
import itertools


def small_roots(f, bounds, m=1, d=None):
    if not d:
        d = f.degree()

    R = f.base_ring()
    N = R.cardinality()
    
    k = ZZ(f.coefficients().pop(0))
    g = gcd(k, N)
    k = R(k/g)

    f *= 1/k
    f = f.change_ring(ZZ)

    vars = f.variables()
    G = Sequence([], f.parent())
    for k in range(m):
        for i in range(m-k+1):
            for subvars in itertools.combinations_with_replacement(vars[1:], i):
                g = f**k * prod(subvars) * N**(max(d-k, 0))
                G.append(g)

    B, monomials = G.coefficient_matrix()
    monomials = vector(monomials)

    factors = [monomial(*bounds) for monomial in monomials]
    for i, factor in enumerate(factors):
        B.rescale_col(i, factor)

    B = B.dense_matrix().LLL()
    B = B.change_ring(QQ)
    for i, factor in enumerate(factors):
        B.rescale_col(i, Integer(1)/factor)

    H = Sequence([], f.parent().change_ring(QQ))
    for h in filter(None, B*monomials):
        H.append(h)
        I = H.ideal()
        if I.dimension() == -1:
            H.pop()
        elif I.dimension() == 0:
            roots = []
            for root in I.variety(ring=ZZ):
                root = tuple(R(root[var]) for var in f.variables())
                roots.append(root)
            return roots

    return []


c1,leak1,n1 = (89623543982221289730635223555830551523170205418976759060541832483843039074358160566735322009158596405712449020903311144480669706226166537602750967447480664875090686428406188847601970724994074417752345460791736191511081890913041143570455636020205647345764692062144226011846336769477026234106683791286490222089, 138474880017294332349992670187778287774153347391371789199005713563195654993662610111557185709277805165708109047494971468100563949333712521647405765501704478862377527360106399421209690341743821320754482338590671565510629203215009008479290995785318405211007685664887994061938667418220613430135743123498167435264, 146331610798417415036517077006943013321623040860385791423062775325646472298267580898028515394910588437521335092742913111680737790430660749825981979147191282007208147041227246620008377726207734522466015971515317594545750944838673018946440525615131606652748549901880641896940968837669894325535750125282351577689)
c2,leak2,n2 = (5473961166821344576614003060897848014482672788904094340704447882490091115468180944569409159343222459801235179587721232166576530621751748850763430788036935832653535110975154800191323351333883661451331971042214143454441651165718504131976920077768864850035471790911190772583977173388975105970866592974077361193822302653046511418190410043729876062517148438923211673300268277037622337403526399584759202097925983596261279676101079771530118525540842499517622478819211528345668513680064744443628779623340175578509413636950545134641050948185944279029949957748464529075830770617236599864271566534714755373562527112224962839980,62964793504732923650344975634773688108135580826064134090114181449607062497690184718845295432644650580930430061411603385577783897575232298084007041511817031640186953023971498914096209984730,20748652069632848434897928314437138341436264859802586939154590237186029244907936870477844563166827587536149170710720365760129683024401957095447466056746469055173897234659911291443605912459271248059341147358511860537769587963189092648473894868209838600346115919726589891777340166174017389513260737891557712152871714337946675533597049874155202056200170954033849176655928144354665553271709442011723088448485570394208728775665739819536229908847043007472178803394055783543378990699834066614262050119443421709878598533329555838915158259138297060574425019923291353077080236769586821808150397875920110335669136563171420068201)
c3,leak3,n3 = (34640310217688693418173336791306022698488916505988760907493665070072623574363578354500529023855888624978101429772253437880445815006839767802433777006836665709335479076676231470534690281412388704665083311568028710188940132495410474044569100181764053297307413009214044407982980600917158732129850605715306726034, 3763587651775261955566046684899146246387485307521708557610018711932791630073528010801142052497, 94848869174430082173244966077736519396702141299429965725051314270443078621842166791082354594193554380275167898342497998871366256044865879909218309960595691008663632410356093966762639308253848450178310347612630814852054763933063313537694449475061227647475480417779126252294793767003555255527593551612032661749)
e1,e2,e3 = 149,65537,65537


############################################# task1
k1 = e1*leak1 // n1 + 1
PR.<x,y> = PolynomialRing(Zmod(e1*leak1))
f = 1 + k1*((n1+1)-y) - e1*x
bounds = (2^222,2^513)

res = small_roots(f,bounds,m=2,d=2)
leak = int(res[0][1])

PR.<x> = PolynomialRing(RealField(1000))
f = x*(leak-x) - n1
ph = int(f.roots()[0][0])


PR.<x> = PolynomialRing(Zmod(n1))
f = ph + x
res = f.small_roots(X=2^(222+6), beta=0.499,epsilon=0.02)[0]
p1 = int(ph + res)
q1 = n1 // p1
d1 = inverse(e1,(p1-1)*(q1-1))
m1 = pow(c1,d1,n1)


############################################# task1
if(0):
    PR.<x> = PolynomialRing(Zmod(n2))
    pl = var('pl')
    p0 = solve_mod([pl*(leak2-pl) - n2  == 0], 2^624)
    for i in tqdm(p0):
        temp = int(i[0])
        f = 2^624*x + temp
        f = f.monic()
        res = f.small_roots(X=2^(1024-624), beta=0.499,epsilon=0.05)
        if(res != []):
            print(res,i)
p2 = 2^624*1818858780662674672546519234621144829011634239453991533158800384602749900390376290902354433158869501621068317141437803547 + 30799806171826831530692477758473366666506107409058776239288103697521834047472422841398780886795811096950227412499497614896605408091510012455390741008241034524397897872311534501791582888829
q2 = n2 // p2
d2 = inverse(e2,(p2-1)*(q2-1))
m2 = pow(c2,d2,n2)


############################################# task1
leak3 = leak3 << 200
LEAK = bin(leak3)[2:].zfill(512)
def find(ph,qh,h):
    pM = int(ph + (512-h)*"1",2)
    qM = int(qh + (512-h)*"1",2)
    pm = int(ph + (512-h)*"0",2)
    qm = int(qh + (512-h)*"0",2)

    if(h == 512 - 200):
        PR.<x> = PolynomialRing(Zmod(n3))
        f = pm + x
        res = f.small_roots(X=2^200,beta=0.499)
        if(res != []):
            p3 = int(pm + int(res[0]))
            q3 = n3 // p3
            d3 = inverse(e3,(p3-1)*(q3-1))
            m3 = pow(c3,d3,n3)
            print(long_to_bytes(int(m1+m2+m3)))

    if(pM*qM < n3 or pm*qm > n3):
        return
    
    if(LEAK[h] == "0"):
        find(ph+"1",qh+"1",h+1)
        find(ph+"0",qh+"0",h+1)
    else:
        find(ph+"1",qh+"0",h+1)
        find(ph+"0",qh+"1",h+1)

find("1","1",1)

这样就可以解出来了

1
XYCTF{___y0u_k0nW_h0w_t0_s01v3_c0pP3r_th15_15_y0r_fl@9_hahahaha!!!___}

new_LCG(未解决)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
from Crypto.Util.number import *
import random
from secrets import flag

p = getPrime(512)
q = getPrime(512)
r = getPrime(512)
n = p * q * r


class LCG1:
    def __init__(self, seed, a, b, m):
        self.seed = seed
        self.a = a
        self.b = b
        self.m = m
        self.sum = 0

    def next(self):
        old_seed = self.seed
        self.seed = (self.a * self.seed + self.b * self.sum) % self.m
        self.sum += old_seed
        return self.seed


class LCG2:
    def __init__(self, seed, q, A, B):
        self.E = EllipticCurve(GF(q), [A, B])
        self.P = self.E.lift_x(seed)
        self.b = self.E.random_point()

    def next(self):
        self.P = self.P + self.b
        return self.P[0]


a1 = random.randint(1, p)
b1 = random.randint(1, p)
seed1 = random.randint(1, p)
lcg1 = LCG1(seed1, a1, b1, p)
c1 = []
for _ in range(10):
    c1.append(lcg1.next())

a2 = random.randint(1, q)
b2 = random.randint(1, q)
seed2 = random.randint(1, q)
lcg2 = LCG2(seed2, q, a2, b2)
c2 = []
for _ in range(10):
    c2.append(lcg2.next())

c = bytes_to_long(flag)
e = 65537
print(n)
print(pow(c, e, n))
print(c1)
print(c2)
# 942554394956393500634473023924044851150783066435925660508624376974971108656861080872622432250172571195245180102507380675343264066303507696268870722959770362631674931170602993210221083436437860191861911457384526742569208842886612504579678703976889217504241741044075116270718940025586448491942058697669033418724145042156461740336592337509609124425828725269151627786668070531098444935129266626770404736852607352075247856808563388127774523912002202264558855255067503
# 91351185520045025851535940537599785616890151570421939971146348618267656786110090770321857244701820126026227283965934212135946431643320325513590505155214070540638751565105300361430272638957420276596026161454413739823593506516275224444666187442238624864548263927274591212614561916913851855552516864387460946267629794664216228596534684933791607740725160394841711539767932339281214673649553407414347293480522175832736301571839298158011533849603878482322619858083471
# [6924229081976334180193477951417117275396656434968000032228908231511246053064833236257422745299036986875244562025221130619850904830372215788197314906896784,707045810464337488125013716300756405499020414540801863434513087687914538170573314824134496890600422837133767094273649381435979038909605432188919586751472,561487665739111774897165274560908487232457333748910467998343202097778699925650682704996443560224288857862513676706660506594465853704042586896087391214886,6498834369085375452441121562339384727357898216850540864190840194924515286757125433756518026123451611578553656133012172518080309106483207567929943790044792,5508345401684913940610183958526398635406187349043368834080838153611810896629693027245511688366776749176652858929409374912959736262162942801190344337268446,7604410082265211154108357446507297790451766698177313130672954202813796888988719242951127448112228332967892794819415211618572734294964346056056171483002307,7699815879242527638422887386550759485127768822609011364311314299885418068889791030639324882736871756700299169635780542149704586720216395186814592666988591,829748131720382599696653359722612708514830904084605048590882951300049701148883021283243506081300427041733299385325284399270633917941134488957784480285437,7084115400374950827522650500486495223539292992998875483730758098005030106055310282589342193536381973309924074043955222228738842206417828828756951777504457,7482796067314266426215648326036921955183807741134787613584977300821023398375789725848056657250086288687570875979072368004217788222537115232191230702833854]
# [12573984103581521249597169818949825744876735847170990673204303602848066091917704946653820386665801380026230957120354174481948164514637637956459534723582285, 6441954407109995413858792101472089558106780628459991101662507565699664222341697230094798036088532393057448200220905589679548875702178737462785403325555226, 11684244745641367106386196774447204674089853123966422387024948921795099192025069760680924547214190425118261001002764397184950251157744938735586522727499550, 10396243416373326695473843427139385116708652845789644861965876346553795313454773668473030130335970707089781482749749170266279229263892370064669233541305377, 9090748241360606371310281608818966855338110969397659720953951845805983771894064629343960530245792700858927510839835850767728294266738917884471006979663157, 11489848045104749332790333272128633885019156159805805159750174723808043569789257625027794186359921080743368220606914862583644262009648261345452266067697628, 649349258009900424806913260265314442160901414078390702088746248078789581041616487825633046538335114117254875547413590064940767523651802950986197978665018, 6302136940345077947382276151657194124073457559487274425879887978386901058162385833414602346299055653879087077862824771863209271498552774720708307840705334, 5844526398244645236473089500608731415060125566027525405618000580381149761653744142808567706048834618328671311836990498943019718294135733114642775270792763, 4834548043993868659061606699822957422840040425976833628462093089330507589865407793951971491111695171201542345470702059513427268037868859282999222070054388]

Reverse

聪明的信使

​ 一眼古典密码，直接打开ida，按f5，对字符串进行解密就可以了

1
flag{Y0u_KnOw_Crypt0_14_v3ry_Imp0rt@nt!}

喵喵喵的flag碎了一地

​ 在程序开头处找到第一处flag，说第二处flag在function中，我们很容易找到，然后根据提示，就可以知道第三处跟function互相引用（xref）了，所以找到对应的function718，是在一个数字下，读出flag即可

1
XYCTF{My_fl@g_h4s_br0ken_4parT_Bu7_Y0u_c@n_f1x_1t!}

Misc

熊博士

1
CBXGU{ORF_BV_NVR_BLF_CRZL_QQ}

​ 看出来是古典加密，根据前五位XYCTF就可以推断出加密方式了，是两个位置上的ascii码加起来永远不变，容易得出flag

1
XYCTF{liu_ye_mei_you_xiao_jj}

签到

​ 第一题！直接发给公众号获得flag

1
XYCTF{WELCOME_TO_XYCTF}

EZ_Base1024*2

base2048在线解密：

Encode and Decode Base2048 Online Tool

得出结果

1
XYCTF{84ca3a6e-3508-4e34-a5e0-7d0f03084181}

真>签到

有手就会，把附件放进01编辑器中，读取前面的flag就可以了

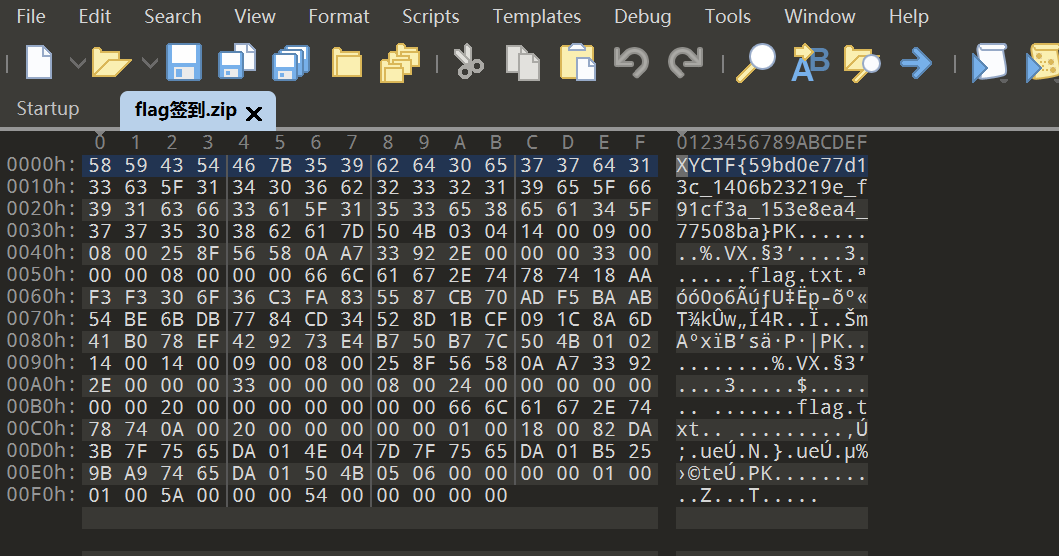
读取flag

1
XYCTF{59bd0e77d13c_1406b23219e_f91cf3a_153e8ea4_77508ba}

Osint1

​ 这题给了一个滨海新区的照片，本来因为是天津市的，但是不是，后来在百度识图在一个网址上找到了用户的ip为江苏，再进一步查询发现该地点在江苏省南通市海安区，在滨海东路上，外面的海是黄海。

得到flag：

1
xyctf{江苏省|南通市|滨海东路|黄海}