2024H&NCTF

Posted on | In |

更新一下，刚学crypto时打的比赛，做了两个crypto题

Crypto

BabyPQ

进入端口，得到我们的n和phi

我们已知 

1
2
3
4
5
6
n= 49591977487629594945496373438511006111775528534545574233225149697175329748553605568368963756920661135425024807876418929312382617151908592963419269275343863166615811689723484880951512308750038206562522283030655840533891416358727464163458870504250389804872146353448401968369599477838528162180039236966333218441 
phi=49591977487629594945496373438511006111775528534545574233225149697175329748553605568368963756920661135425024807876418929312382617151908592963419269275343849077869099594315012439173163522525652948396478054170312697035143915818749650675143752409819847997605469066583155373813828741099849410231696320264247769492

from sympy import *
x,y= symbols('x,y')
print(solve([x*y-n,(x-1)*(y-1)-phi],[x,y]))

通过解方程，我们就可以得到我们的p和q

然后输入我们的p就可以了，得到flag

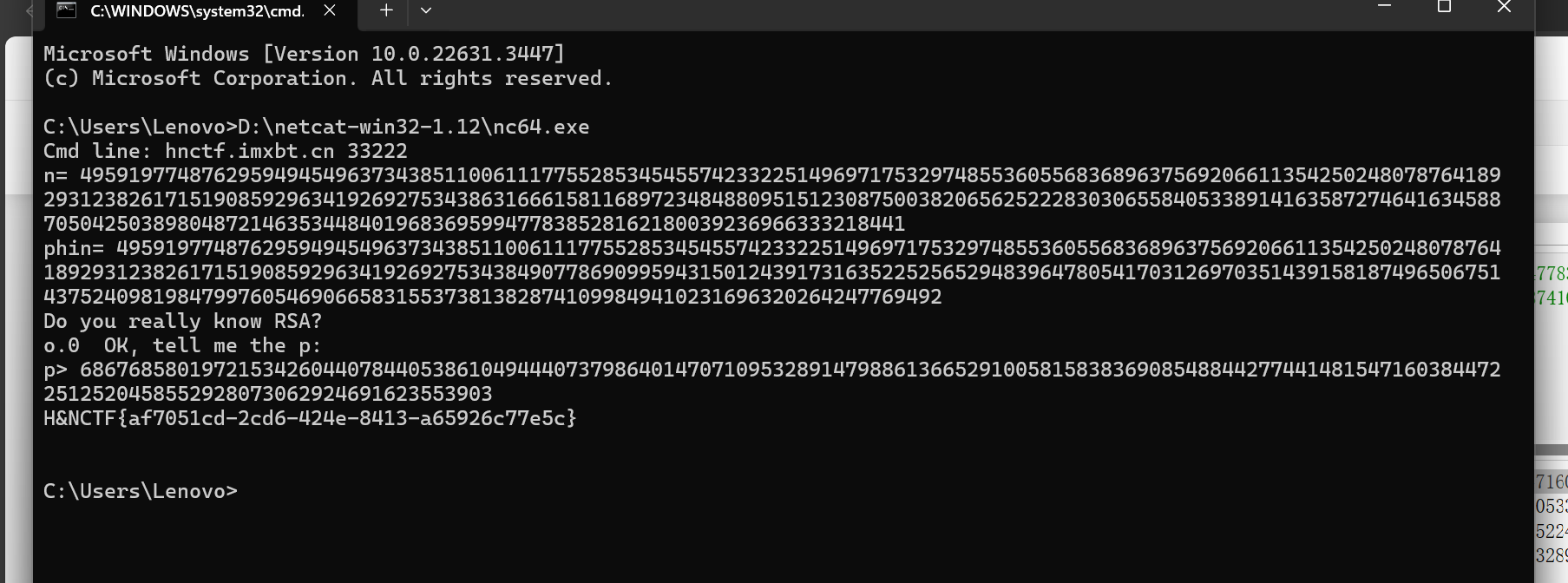
flag的值为：H&NCTF{af7051cd-2cd6-424e-8413-a65926c77e5c}

MatrixRSA

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from Crypto.Util.number import *
import os

flag = b"H&NCTF{??????????????}" + os.urandom(73)

p = getPrime(56)
q = getPrime(56)
n = p * q

part = [bytes_to_long(flag[13*i:13*(i+1)]) for i in range(9)]

M = Matrix(Zmod(n),[
    [part[3*i+j] for j in range(3)] for i in range(3)
])

e = 65537
C = M ** e
print(f"n = {n}")
print(f"C = {list(C)}")

"""
n = 3923490775575970082729688460890203
C = [(1419745904325460721019899475870191, 2134514837568225691829001907289833, 3332081654357483038861367332497335), (3254631729141395759002362491926143, 3250208857960841513899196820302274, 1434051158630647158098636495711534), (2819200914668344580736577444355697, 2521674659019518795372093086263363, 2850623959410175705367927817534010)]
"""

文献题，查阅关键词Matrix和RSA就可以找到对应的论文

我们只需要将我们的欧拉函数进行替换就可以了

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from gmpy2 import *
from Crypto.Util.number import *
import numpy
p=56891773340056609
q=68964114585148667
n=p*q
e=65537
phi=(p**2-1)*(p**2-p)*(q**2-1)*(q**2-q)
d=invert(e,phi)
C = [(1419745904325460721019899475870191, 2134514837568225691829001907289833, 3332081654357483038861367332497335), (3254631729141395759002362491926143, 3250208857960841513899196820302274, 1434051158630647158098636495711534), (2819200914668344580736577444355697, 2521674659019518795372093086263363, 2850623959410175705367927817534010)]
#C = Matrix(Zmod(n),[
 #   [(1419745904325460721019899475870191, 2134514837568225691829001907289833, 3332081654357483038861367332497335), (3254631729141395759002362491926143, 3250208857960841513899196820302274, 1434051158630647158098636495711534), (2819200914668344580736577444355697, 2521674659019518795372093086263363, 2850623959410175705367927817534010)]
#])
#print(numpy.linalg.matrix_power(C, d) )

print(d)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import numpy as np
def mod_matrix_multiply(A, B, n):
    # 在模 n 的有限域上计算矩阵乘法
    C = np.dot(A, B) % n
    return C

def mod_matrix_power(A, power, n):
    # 计算矩阵 A 的幂
    result = np.eye(len(A), dtype=int)  # 创建单位矩阵
    while power > 0:
        if power % 2 == 1:
            result = mod_matrix_multiply(result, A, n)
        A = mod_matrix_multiply(A, A, n)
        power //= 2
    return result

C = [(1419745904325460721019899475870191, 2134514837568225691829001907289833, 3332081654357483038861367332497335), (3254631729141395759002362491926143, 3250208857960841513899196820302274, 1434051158630647158098636495711534), (2819200914668344580736577444355697, 2521674659019518795372093086263363, 2850623959410175705367927817534010)]
n=3923490775575970082729688460890203
d=62943786360045783729872631416452305443726414552945421595258301764271056603535020810729178005843237877043494288357220800501261583450113
print(mod_matrix_power(C,d,n))

这样我们就可以求出原来的矩阵了，然后我们进行字符转化就可以得到我们的flag了

1
H&NCTF{58bff5c1-4d5f-4010-a84c-8fbe0c0f50e8}