供南开大学计算机学院和网络空间安全学院期末复习使用

免责声明：本人水平有限，笔记难免有错误，请理性使用，切莫完全相信本笔记的所有内容。

分值分配：课上随堂测试考核(10%)、研讨内容(10%)、实验内容考核(40%)和期末考试(40%)

期末考试：30道选择题（每小题2分）4道简答题（每小题5分）2道解答题（每小题10分）

第四章监督学习

知识点

机器学习基本概念

图像数据类别分类，文本数据情感分类

机器学习的三种类型：监督学习，无监督学习和强化学习，其中监督学习和无监督学习合起来叫作半监督学习

监督学习就是提供了对应的，无监督学习就是不提供对应的，强化学习就是在环境交互中进行学习

监督学习的几个重要因素：标注数据——学什么，学习模型——怎么学，损失函数——学到了吗？

损失函数：

我们的训练集共有组训练数据，分别是，就是我们根据我们的映射函数，我们去与我们的进行对比，找出中间的差值，这样就是我们的损失函数。

损失函数最小化—— 常见的损失函数：

损失函数：平方损失函数：绝对损失函数：对数损失函数：我们的机器学习的训练过程，就是先训练数据集，得到映射函数，然后我们通过在测试数据集上测试我们的映射函数，得到一个较好的结果后，我们再将其运用于我们的未知的数据集上

对应着有两种风险：

一个是经验风险，就是训练集中数据产生的损失。经验风险越小说明学习模型对训练数据拟合程度越好
一个是期望风险，当测试集中存在无穷多数据时产生的损失。期望风险越小，学习所得模型越好

我们的映射函数的训练目标就是让经验风险最小化，如下所示：还需要让期望风险也最小化，如下所示：

训练集上表现	测试集上表现
经验风险小	期望风险小	泛化能力强
经验风险小	期望风险大	过学习（模型过于复杂）
经验风险大	期望风险大	欠学习
经验风险大	期望风险小	“神仙算法”或“黄粱美梦”

为了防止过拟合，让结构风险最小，我们在经验风险中加上惩罚项，在最小化经验风险与降低模型复杂度之间寻找平衡

生成模型与判别模型

监督学习方法又可以分为生成方法和判别方法，所学到的模型分别称为生成模型和判别模型

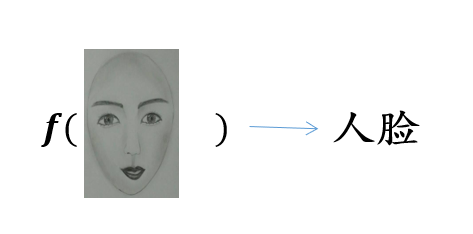
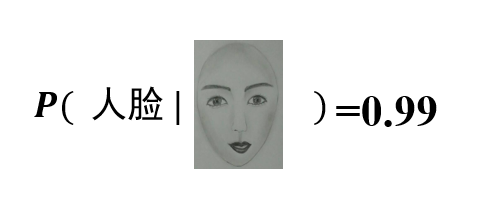
判别模型：判别方法直接学习判别函数或者条件概率分布作为预测的模型，即判别模型。判别模型关心在给定输入数据下，预测该数据的输出是什么。比如说下面的：输入一张图片，我们将其判别为人脸

生成模型：生成模型从数据中学习联合概率分布（通过似然概率和类概率的乘积来求取）

或者，比如说下面的：我们目的是去计算这张照片为人脸的条件概率，而不是去识别

回归分析

一元线性回归

回归模型：

我们有两个未知量，一个是，一个是，我们需要去找到这两个未知数之间的关系，用线性去表示出来

我们在求解的过程当中，会产生一定的误差，为

我们可以利用最小二乘法来解出我们误差最小的情况：

以上就是我们的一元回归的两个参数的求解过程

多元线性回归

回归模型：

其中代表了多元的变量，是一个矩阵，矩阵的行数代表了其变量的个数

均方误差函数：最后的求解公式：

逻辑斯蒂回归

在回归函数中引入函数，是一种非线性回归模型，如下表示：其中，其中的是函数

为什么要使用逻辑斯蒂回归？虽然我们的激活函数是非线性的，但是我们经过对数运算之后，结果居然变成了线性模型

而且，在预测时，可以计算线性函数取值是否大于来判断输入数据的类别归属，这样我们就变成了一个线性的模型！

决策树

大致原理：在分支处做判断，做出我们的决策

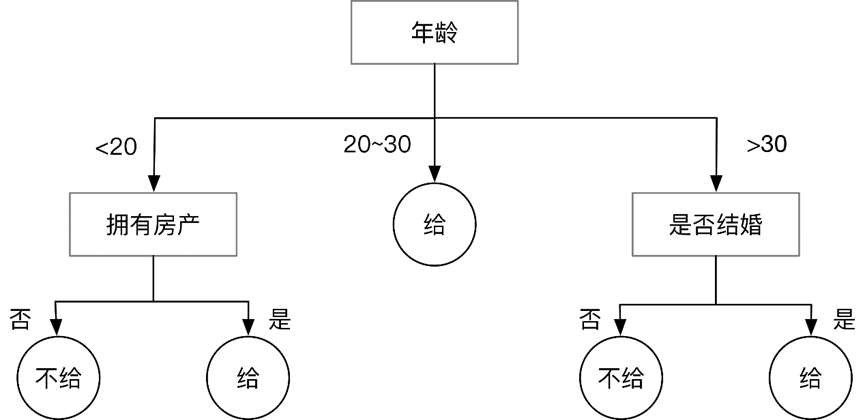
在决策树中起到关键作用的就是信息熵()了

假设有个信息，其组成了集合样本，记第个信息发生的概率为。如下定义这个信息的信息熵：这个值越小，说明我们的信息越确定，纯度越高

对照着上面的图，流程大概是：计算出按照每一类别进行分类产生的信息熵，然后看哪个最大，就按照哪个特征进行区分

线性区别分析(LDA)

用于降维，利用类别信息，将高维数据样本线性投影到低维空间

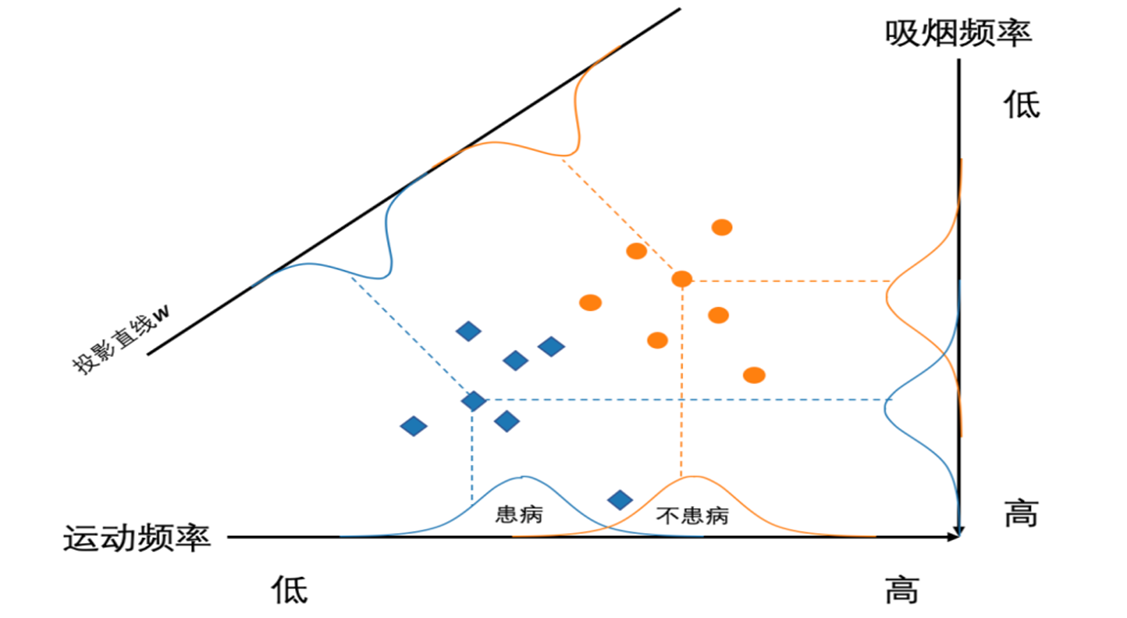
我们可以做到类内方差小，类间间隔大，也就是做到一个良好的分离性能

两个散度矩阵(二分类)：

类内散度矩阵 类间散度矩阵 如何求解？

最大化目标：我们要使我们的函数值最大，也就是最大化分子，最小化分母

我们需要对其进行求解最大值，我们令分母为，然后我们用拉格朗日乘子法去求解我们对其求偏导，令其等于，得到：

最后求解得：

多分类问题(了解即可)：

类内散度矩阵 $其中$ 类间散度矩阵求解过程与二分类相似，我们需要做的是将每一个都使其取值最大，也就是说，每一个都是的一个解

线性判别分析的降维步骤：

计算数据样本集中每个类别样本的均值
计算类内散度矩阵和类间散度矩阵
根据来求解所对应前个最大特征值所对应特征向量，构成矩阵
通过矩阵将每个样本映射到低维空间，实现特征降维

与主成分分析的异同：

	线性判别分析	主成分分析
是否需要样本标签	监督学习	无监督学习
降维方法	优化寻找特征向量	优化寻找特征向量
目标	类内方差小、类间距离大	寻找投影后数据之间方差最大的投影方向
维度	降维后所得到维度是与数据样本的类别个数K有关	对高维数据降维后的维数是与原始数据特征维度相关

Ada Boosting

若一个分类器只能完成整体任务的一小部分，那么我们就称为弱分类器；我们将多个弱分类器结合在一起，就成为了强分类器。弱分类器指的是那些分类准确率低于的算法。

强可学习：学习模型能够以较高精度对绝大多数样本完成识别分类任务

弱可学习：学习模型仅能完成若干部分样本识别与分类，其精度略高于随机猜测

如果已经发现了“弱学习算法”，可将其提升（）为“强学习算法”

两个核心问题：

在每个弱分类器学习过程中，如何改变训练数据的权重
如何将一系列弱分类器组合成强分类器

训练过程

给定包含个标注数据的训练集合

初始化每个训练样本的权重，其中
迭代地利用加权样本训练弱分类器并增加错分类样本权重
- 分别计算每个弱分类器的分类误差，对于第个弱分类器的误差计算如下，其中为示性函数其实就是把该分类器分类不正确的样本权重求和
- 选择最低的分类器
- 计算弱分类器权重：
- 更新样本的分布权重，其中分类正确的样本权重更新为，分类错误的样本权重更新为
- 重新计算每个弱分类器的分类误差，重复上述步骤
以线性加权形式来组合弱分类器
- 得到的强分类器

注意的是，我们在训练新的一轮前，需要调整我们训练数据的权重

支持向量机

经验风险越小，对数据的拟合程度越好，但是一味的降低经验风险容易造成过学习的问题

所以我们通过降低结构化风险，使其最小化的方法来解决我们的过学习问题

一个两类分类问题的最佳分类平面。图中存在多个可将样本分开的超平面。支持向量机学习算法会去寻找一个最佳超平面，使得每个类别中距离超平面最近的样本点到超平面的最小距离最大。

支持向量机认为：分类器对未知数据（即测试数据）进行分类时所产生的期望风险（即真实风险）不是由经验风险单独决定的，而是由两部分组成

第一个就是我们的经验风险，会造成过学习的问题
第二个是我们的置信风险，和我们的支持向量机的训练模型有关

就是说，我们需要先做到经验风险最小，也就是说在训练集上的误差最小；然后我们再做到结构风险最小化，也就是说大间隔为宜

总体的公式是：

我们做的就是，将样本从特征空间映射到高维，使其可分

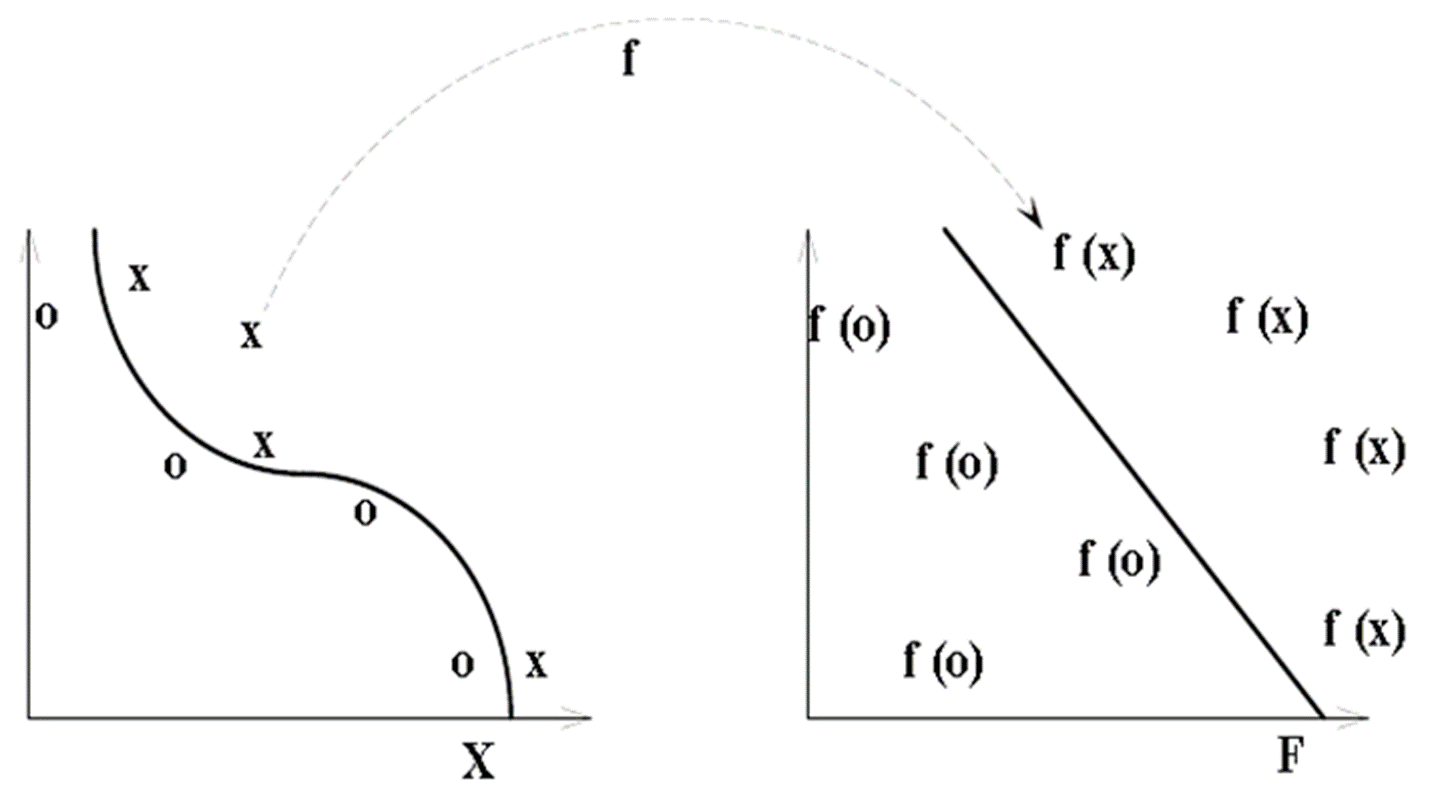
上图我们就解决了原先的样本点不可分的问题，将其映射到高维，这样就可分了

但是随着高维的维数的增加，我们也会出现维数灾难和过拟合的情况

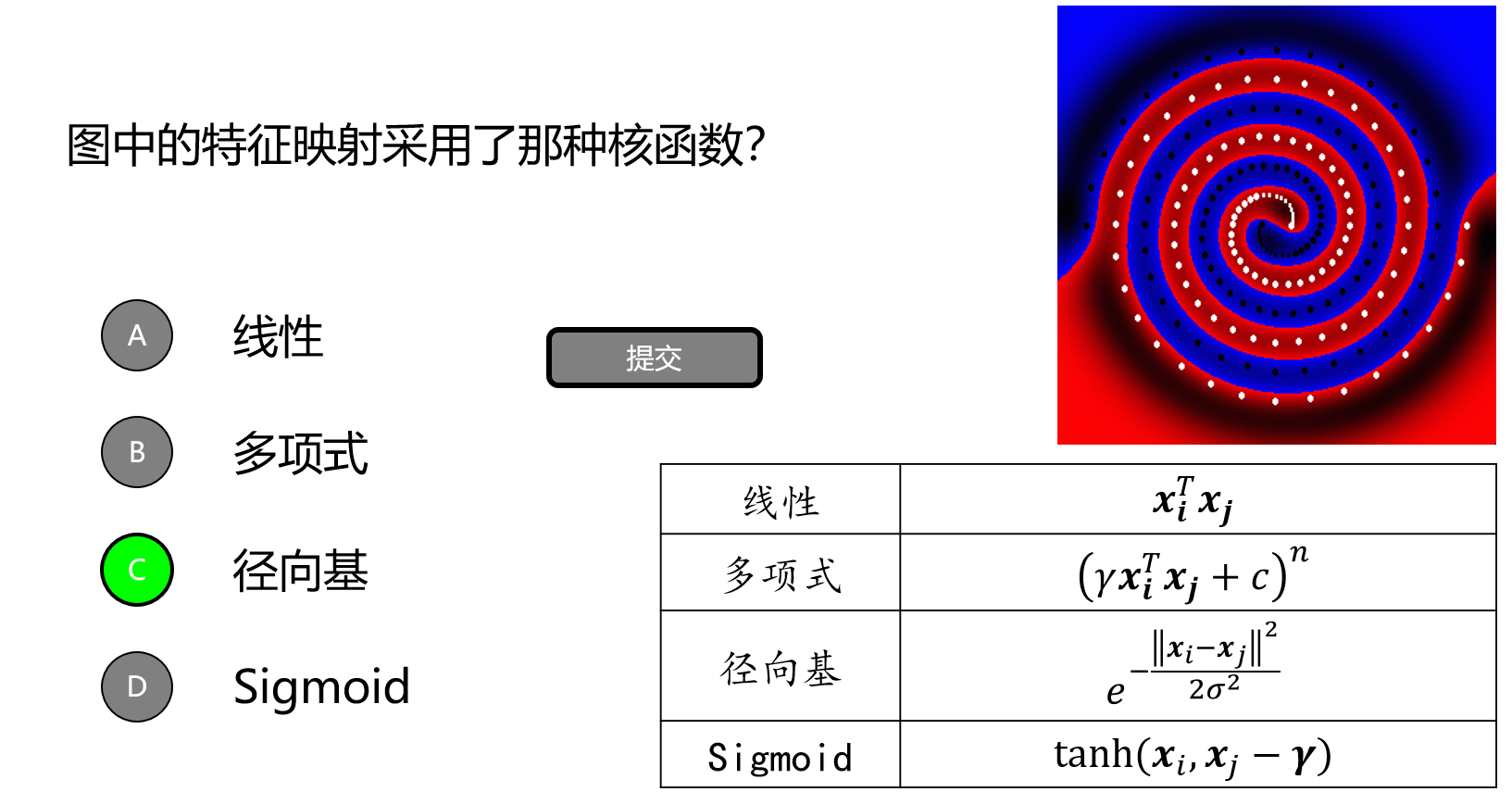
我们怎么解决将不可分转化为可分的呢？我们的映射函数使用了核函数

常见的核函数	对应的表达式
线性
多项式
径向基函数

举个例子：

生成学习模型

判别式学习和生成式学习有什么区别？

判别式学习是，学习到具体的判别线；也就是说我们得到的应该是某一条线，该线左边就是类别1，右边就是类别2
生成式学习是，学到具体的曲线；也就是说我们无法得到具体的分类，只是有我们的曲线，相当于我们求解的是概率，而不是分类

生成学习方法从数据中学习联合概率分布，然后求出条件概率分布作为预测模型，即 $似然概率先验概率$

$后验概率联合概率似然概率先验概率$

第四章 监督学习

知识点