供南开大学计算机学院和网络空间安全学院期末复习使用

免责声明：本人水平有限，笔记难免有错误，请理性使用，切莫完全相信本笔记的所有内容。

分值分配：课上随堂测试考核(10%)、研讨内容(10%)、实验内容考核(40%)和期末考试(40%)

期末考试：30道选择题（每小题2分）4道简答题（每小题5分）2道解答题（每小题10分）

第六章深度学习

知识点

前馈神经网络

神经元

深度学习和机器学习的区别？一个是浅层的学习，一个是端对端学习

我们输入一个需要学习的对象，然后经过我们的端对端学习（一般是卷积等方法进行特征化学习），然后最后输出我们的视觉对象

神经元：有两种形态，一种是抑制状态，一种是激活状态，只有在超过了一定的阈值之后，我们的神经元才会被激活，并且向其他的神经元传递信息，下图就是一个简单的神经元传递的模型：

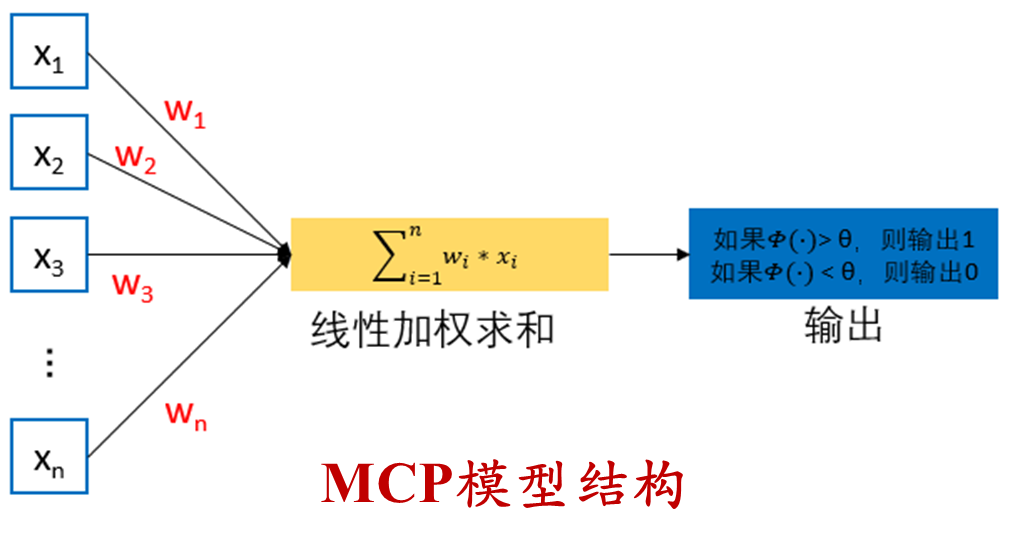
使用函数 $𝛟$ 将加权累加结果映射为或，以完成两类分类的任务：中间利用我们的线性加权求和，来计算出一个值，将我们的结果通过神经元函数来进行映射，映射为或者

神经元是深度学习的基本单位，一般结构如下所示：

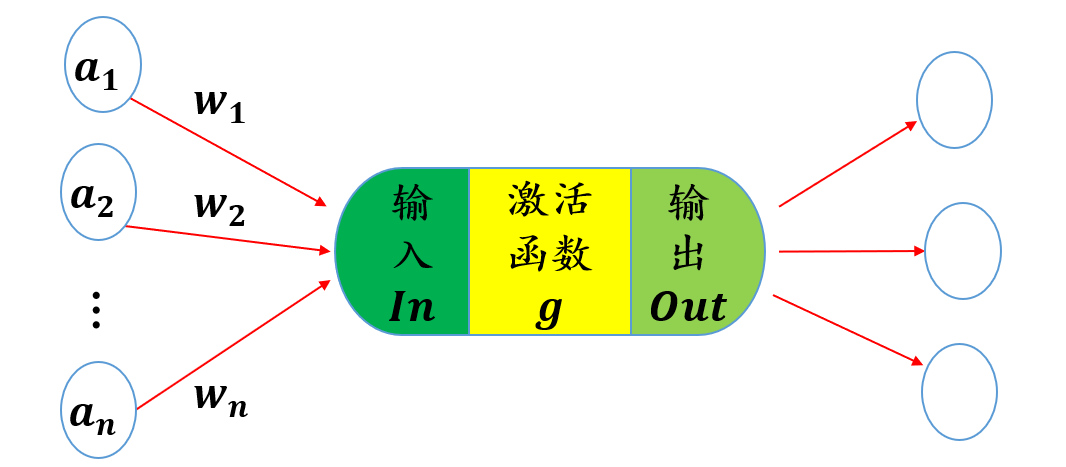
一般来说，首先我们输入我们的信息，然后通过一定的权值进行累加，将我们的累加结果通过非线性变换，通过激活函数去映射到我们的结果上，我们的输出就是

我们的神经元越多，就说明我们的非线性映射越复杂

神经网络使用非线性函数作为激活函数()，通过对多个非线性函数进行组合，来实现对输入信息的非线性变换

常用的激活函数

第一个就是我们的常见的函数，还有我们的函数，函数等等

函数

优点是：该函数的值域在之间，输出的值可以看作是概率值；单调递增，对输入的值的大小没有限制；非线性变化，在的值在附近的时候，我们的函数的值变化最大，反而在取值很大或者很小的时候，我们的函数值变化不是很明显
缺点是：在导数接近的时候，存在梯度消失的问题，并且随着网络深度的增加而变得越来越严重

函数

在原点处的梯度更大，使用该函数更加容易收敛，也面临着梯度消失的问题

函数

也就是说，我们截取掉了负数部分的函数值，将其全部赋值为，这也是一种非线性的变化，可以解决一定的过拟合的问题

函数

一般用在多分类问题中，我们将输入的数据映射到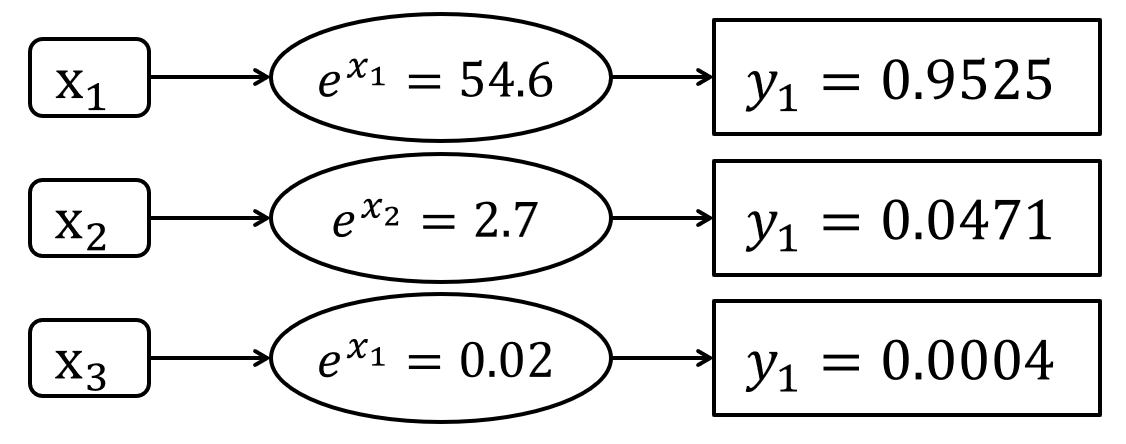的范围内，公式如下：

损失函数

均方误差损失函数

该函数可以输出我们的均方误差

交叉熵损失函数

交叉熵越小，就说明我们两个概率分布越接近

一个良好的神经网络要尽量保证对于每一个输入数据，类别分布概率的预测值与实际值之间的差距越小越好

感知机

我们的前馈神经网络层间“全连接”，即两个相邻层之间的神经元完全成对连接，但层内的神经元不相互连接

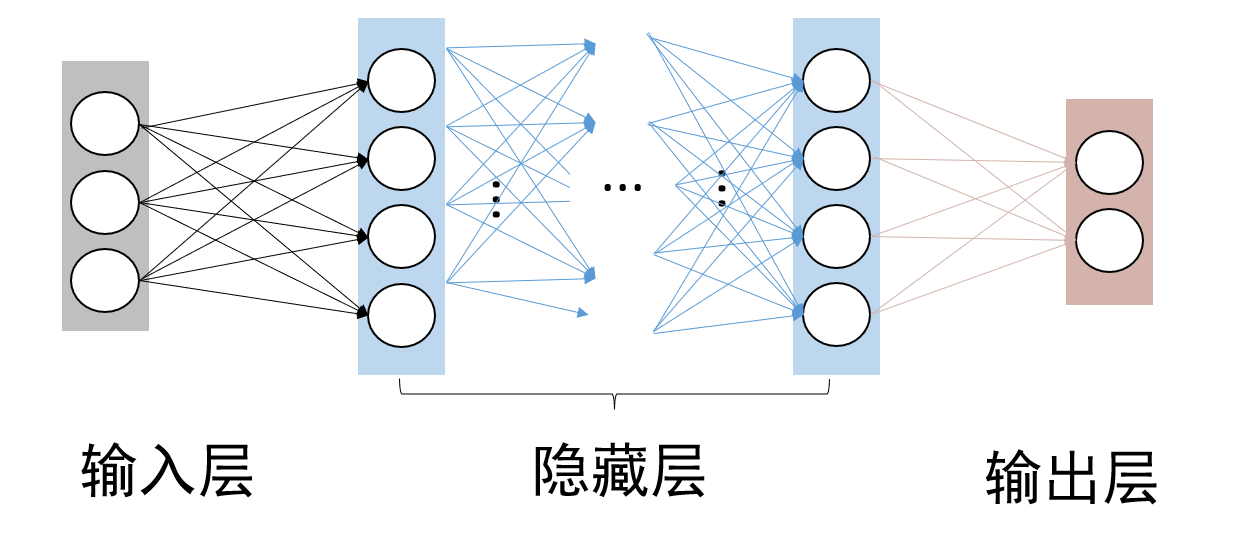
我们的感知机是一种特殊的前馈神经网络，我们没有隐藏层，只有输入层和输出层；但是我们无法拟合过于复杂的数据

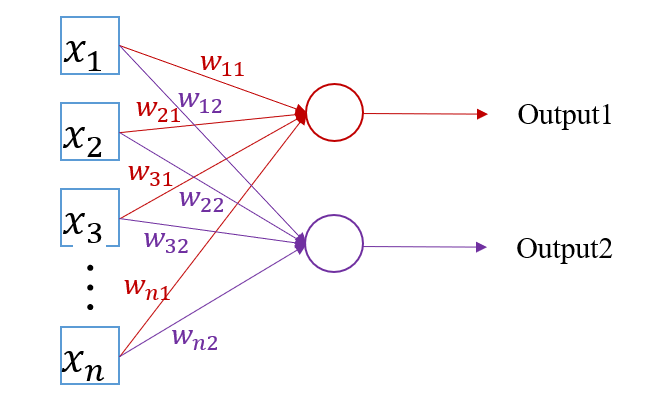
单层感知机

我们的单层感知机可以用来区分线性可分数据

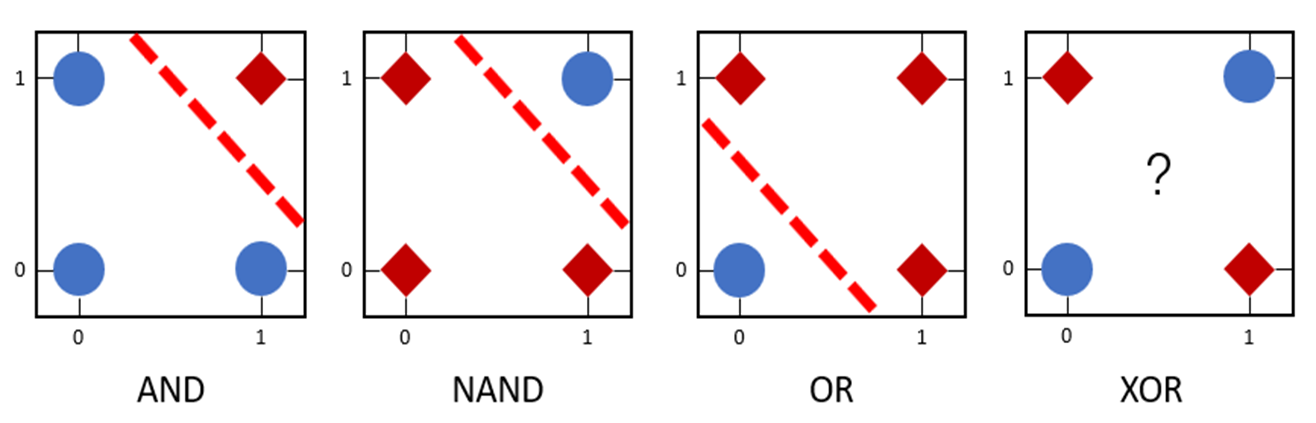
比如说图中的前三个，都是线性可分的，所以我们可以通过我们的单层感知机去进行区分；但是第四个异或我们就不能通过单层感知机去进行区分了

多层感知机

我们可以利用我们的多层感知机去区分我们的线性不可分的数据，比如说上面的异或

多层感知机由输入层、输出层和至少一层的隐藏层构成

各个隐藏层中神经元可接收相邻前序隐藏层中所有神经元传递的信息，加工处理后输出给相邻后续隐藏层中所有神经元
各个神经元接受前一级的输入，并输出到下一级，模型中没有反馈
层与层之间通过“全连接”进行链接，即两个相邻层之间的神经元完全成对连接，但层内的神经元不相互连接

参数优化与学习

我们常见的方法就是：给定一个评分函数，或者说给出一个损失函数，损失函数的差距越小，就说明我们模型的鲁棒性就越好，常用的损失函数有和等，我们优化的目标就是使参数的损失越小，而且我们的参数不复杂

我们还可以通过梯度下降的方法来进行参数的优化在多元函数中，梯度是对每一变量所求导数组成的向量；梯度的反方向是函数值下降最快的方向，因此是求解的方向

误差反向传播：

将误差从后向前传递，将误差分摊给各层所有单元，从而获得各层单元所产生的误差，进而依据这个误差来让各层单元负起各自责任、修正各单元参数

误差传播具体的例子

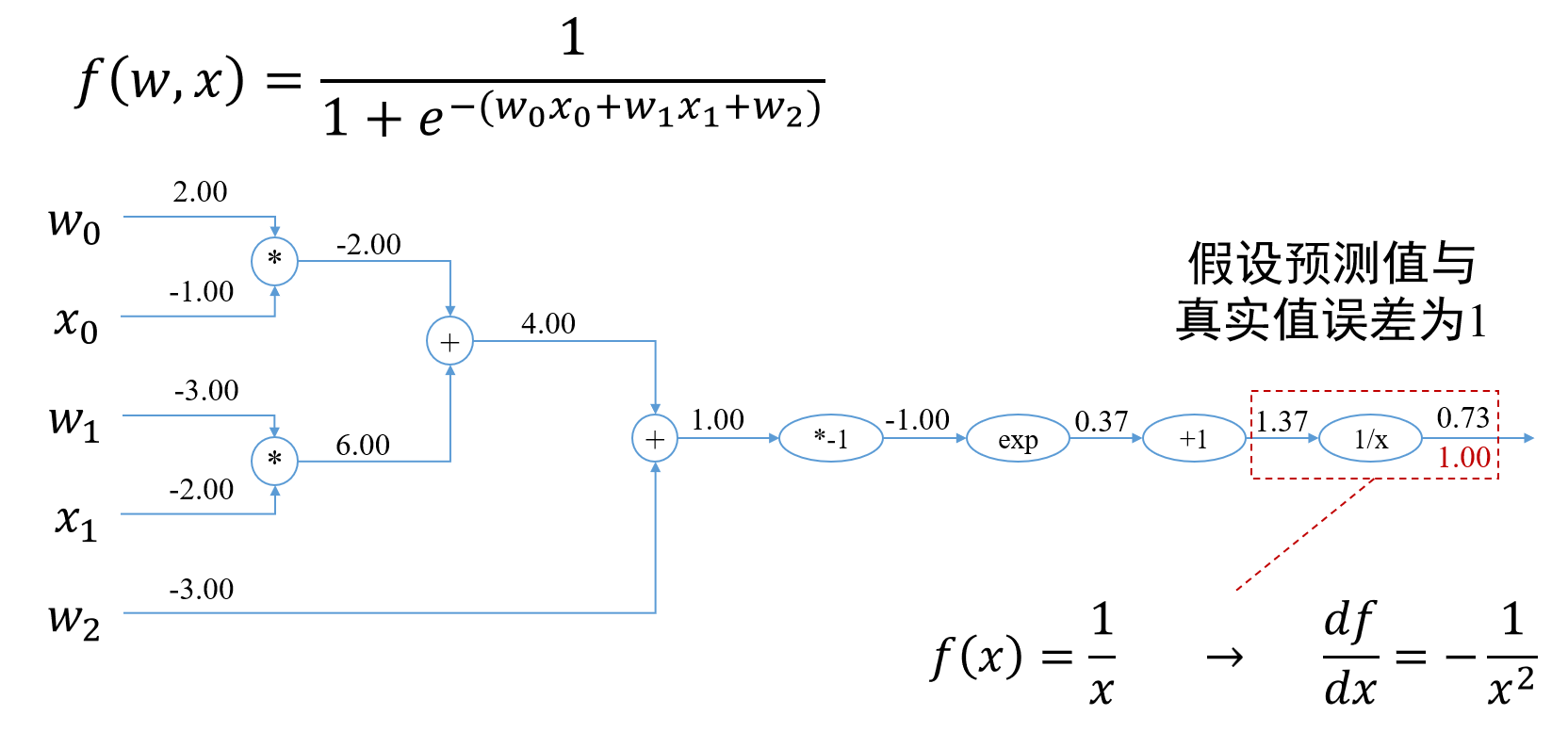
就是通过从后往前的计算，将我们的偏导和误差乘在一起，传递给前面的误差部分，一直传到最前面就可以了

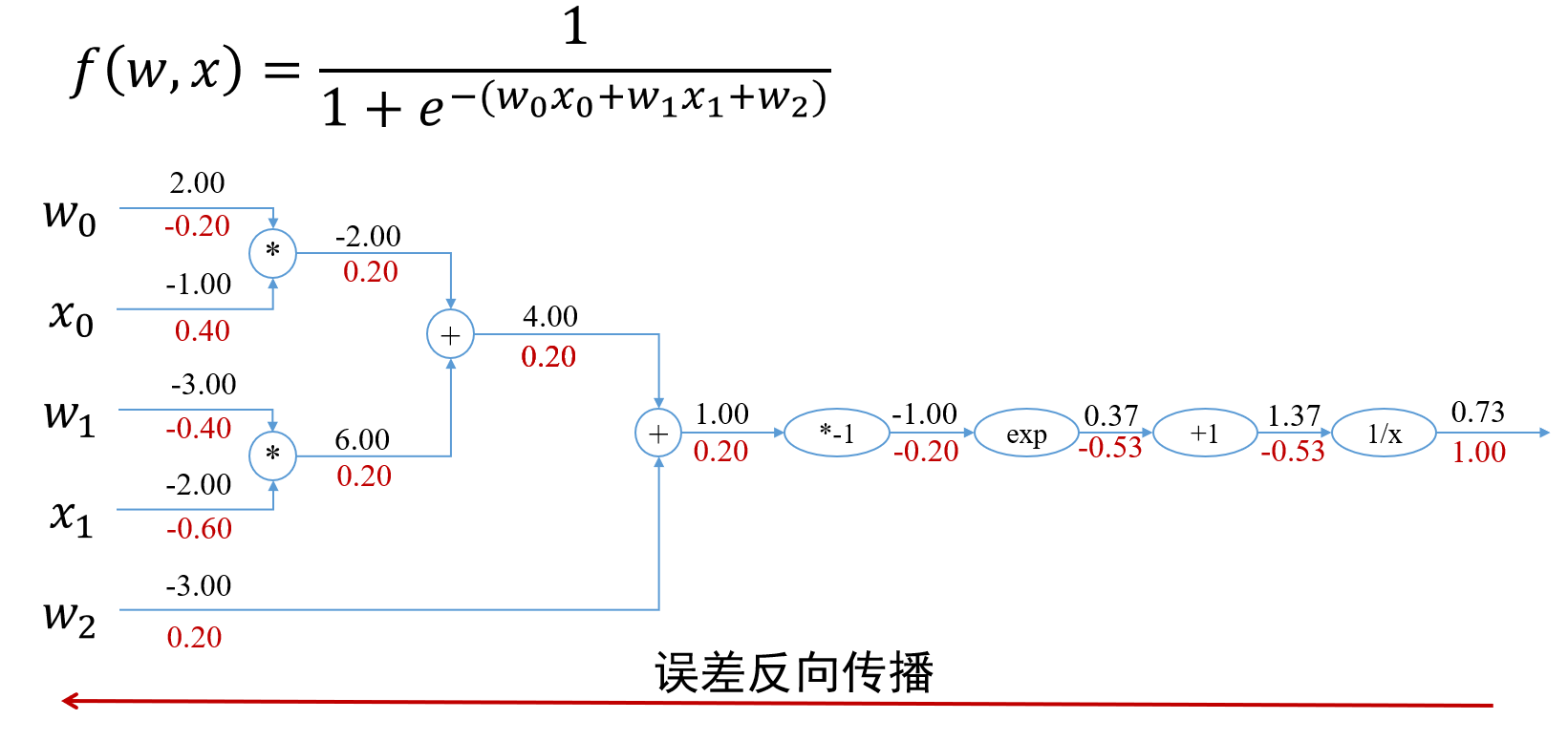
前馈神经网络实例：

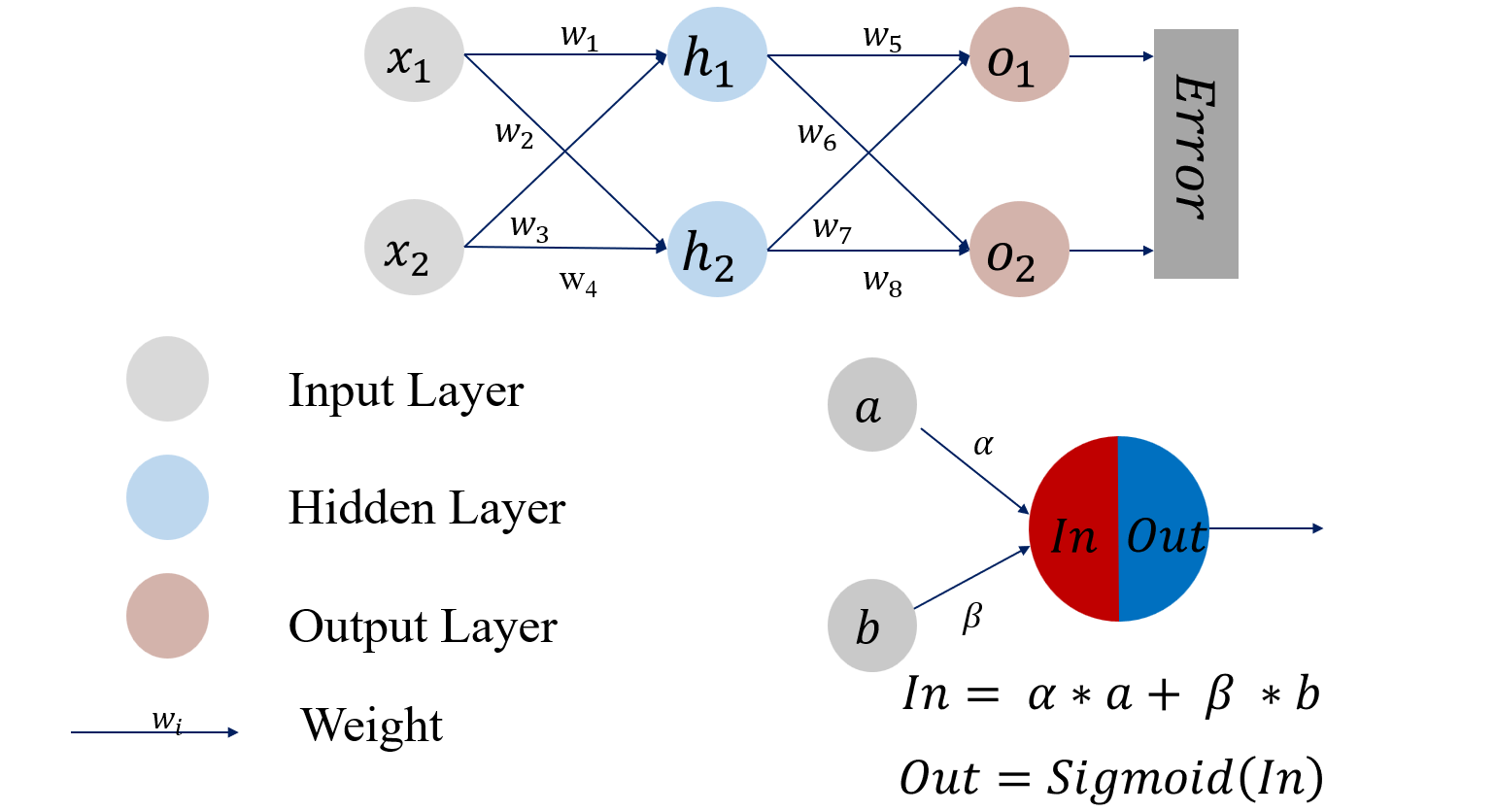
以这个为例，我们对其进行反向传播的梯度计算

以和为例，有如下函数关系

损失函数采取均方差误差，为以和为例，计算梯度

在中，由于与只通过建立关系，所以可以得到其中第一项的值可以直接由对求偏导得到，第二项的值可以由Sigmoid函数的求导公式结合的计算公式得到，注意这里第二项是，第三项可以由的计算公式得到。于是计算上式在计算时，由于是的参数，它通过和均与建立起了联系，所以计算的梯度要分成两部分之和，具体计算公式为之后再继续计算其余偏导数即可。

最后需要对参数进行更新，其中被称为学习率

卷积神经网络

主要结构

前馈神经网络中，输入层的输入直接与第一个隐藏层中所有神经元相互连接

这样所占用的内存很大，所以我们采用卷积的方法，这样就可以学习到对应的知识，还能降低内存的消耗

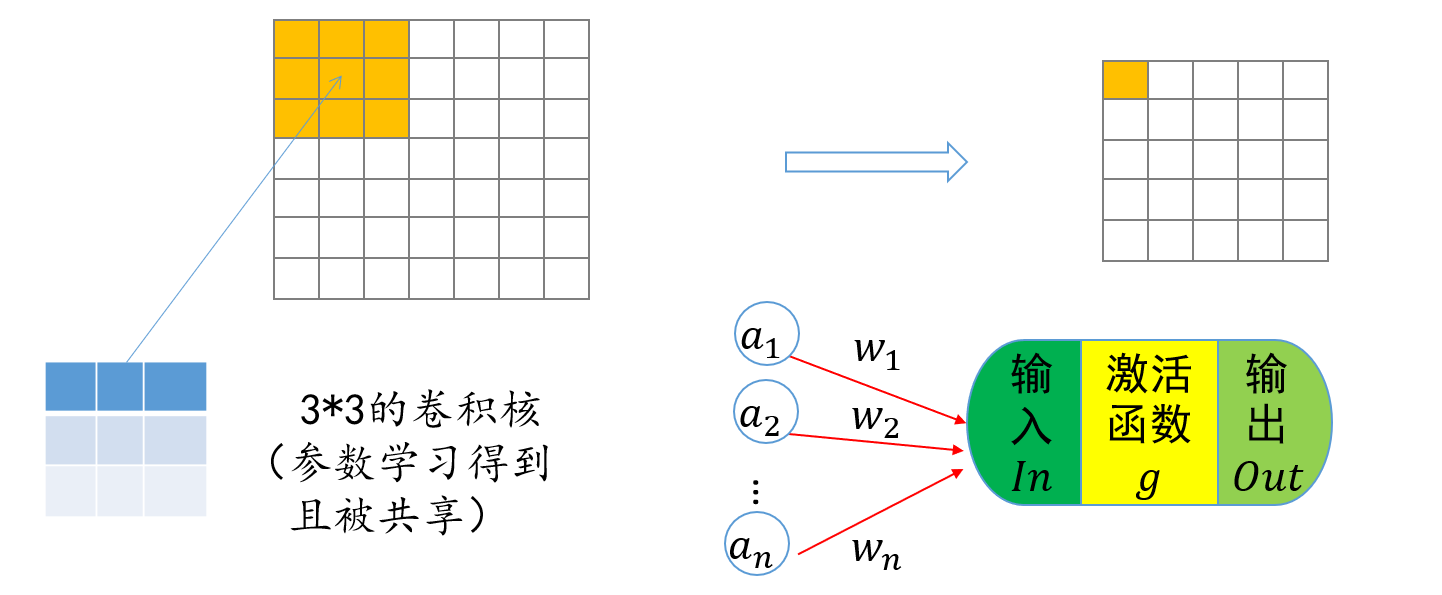
大小的图像，通过大小卷积矩阵以的步长进行卷积操作，可得到大小的卷积结果

如果我们将步长改为的话，这样我们的输出卷积就变成了的结果

有一张()的图像，使用的卷积核，步长为对其进行卷积操作。卷积核在原始图像上从左到右、从上到下进行计算，改变子块区域中的中心像素点值，得到的特征图

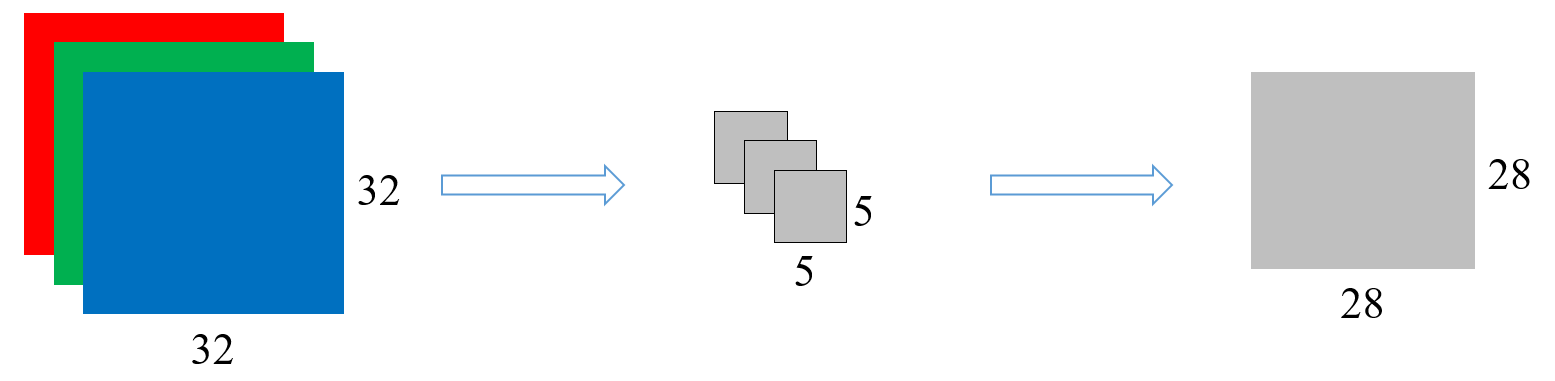
同理，我们继续对剩下的五个卷积核来进行卷积，也可以得到五个的特征图，我们现在就得到了六个的特征图

也就是说，我们有几个卷积核，就会得到几张卷积图。卷积核的数量只会影响最后的卷积图的数量，而不会改变我们卷积得到的维度

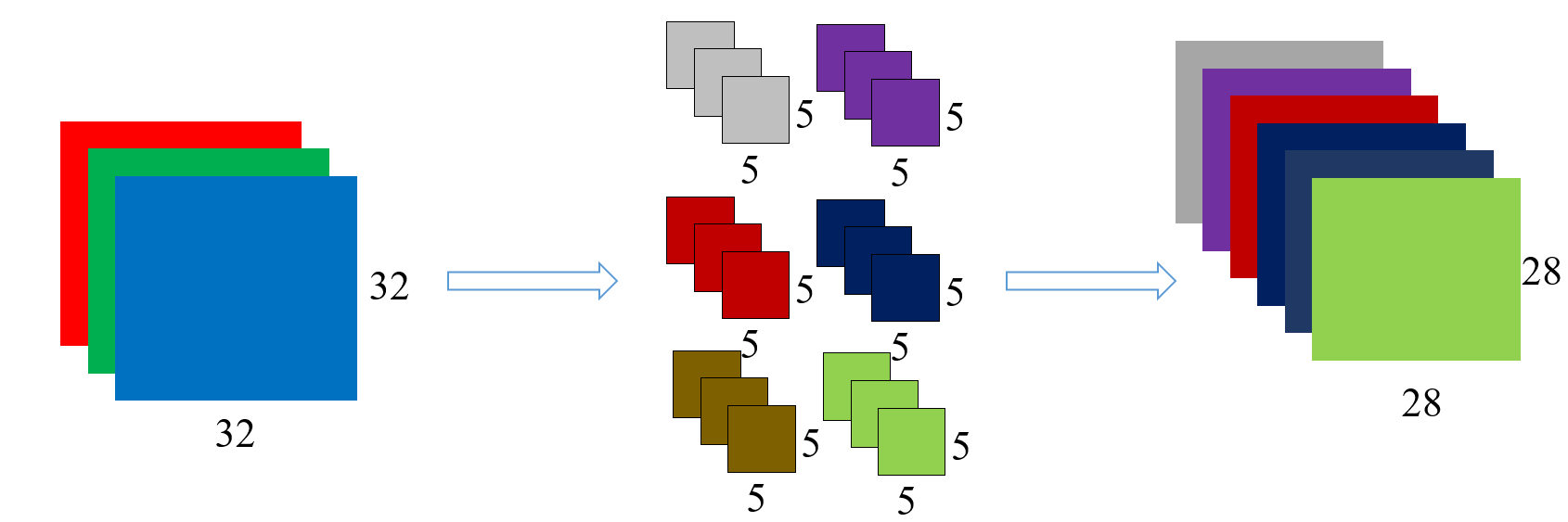
再举一个例子：

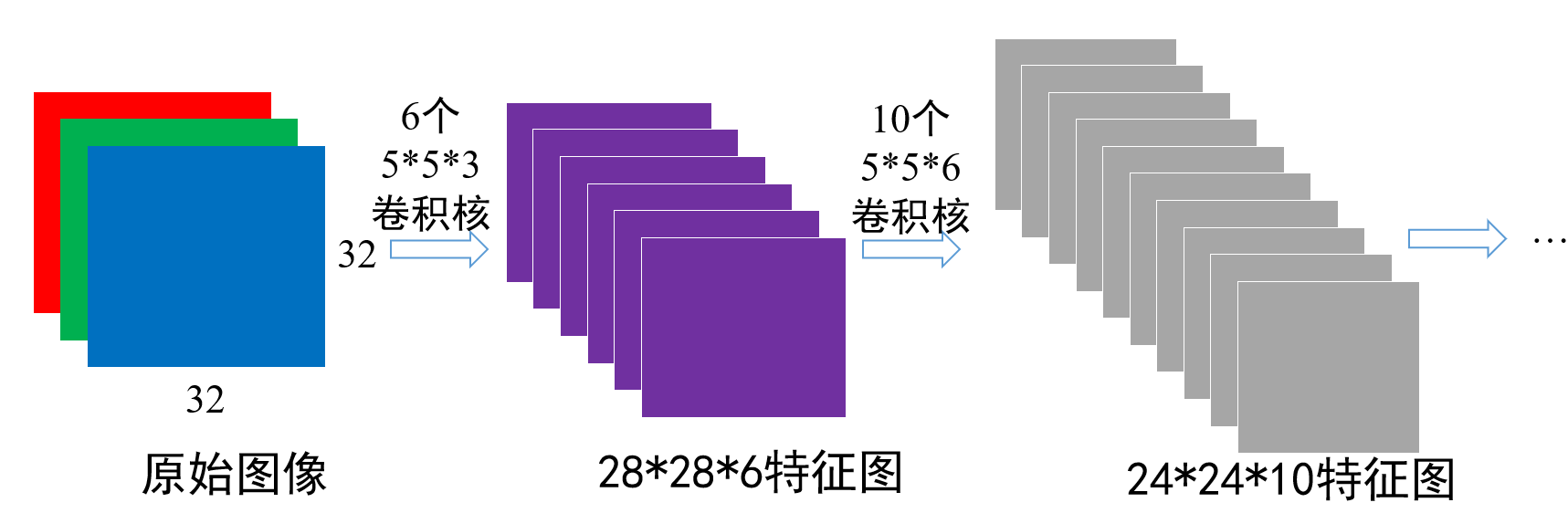
这一个就是，先是通过个卷积核，我们就会生成维度为的特征图，同理后面的也是一样的，所以我们可以看出，特征图的维度并不会影响我们的输出的特征图的数量，特征图的数量都是由我们的卷积核的数量来决定的

池化操作

常见的操作有：最大池化操作；平均池化操作

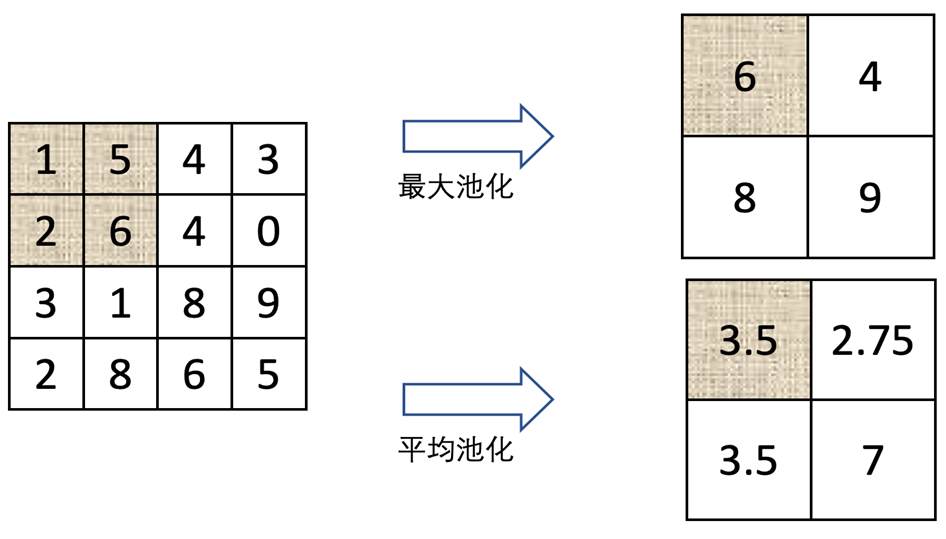
最大池化就是，我们选取我们的卷积核内的最大值进行输出；平均池化就是，我们计算我们卷积核内的平均值进行输出

池化操作对卷积结果特征图进行约减，实现了下采样，同时保留了特征图中主要信息

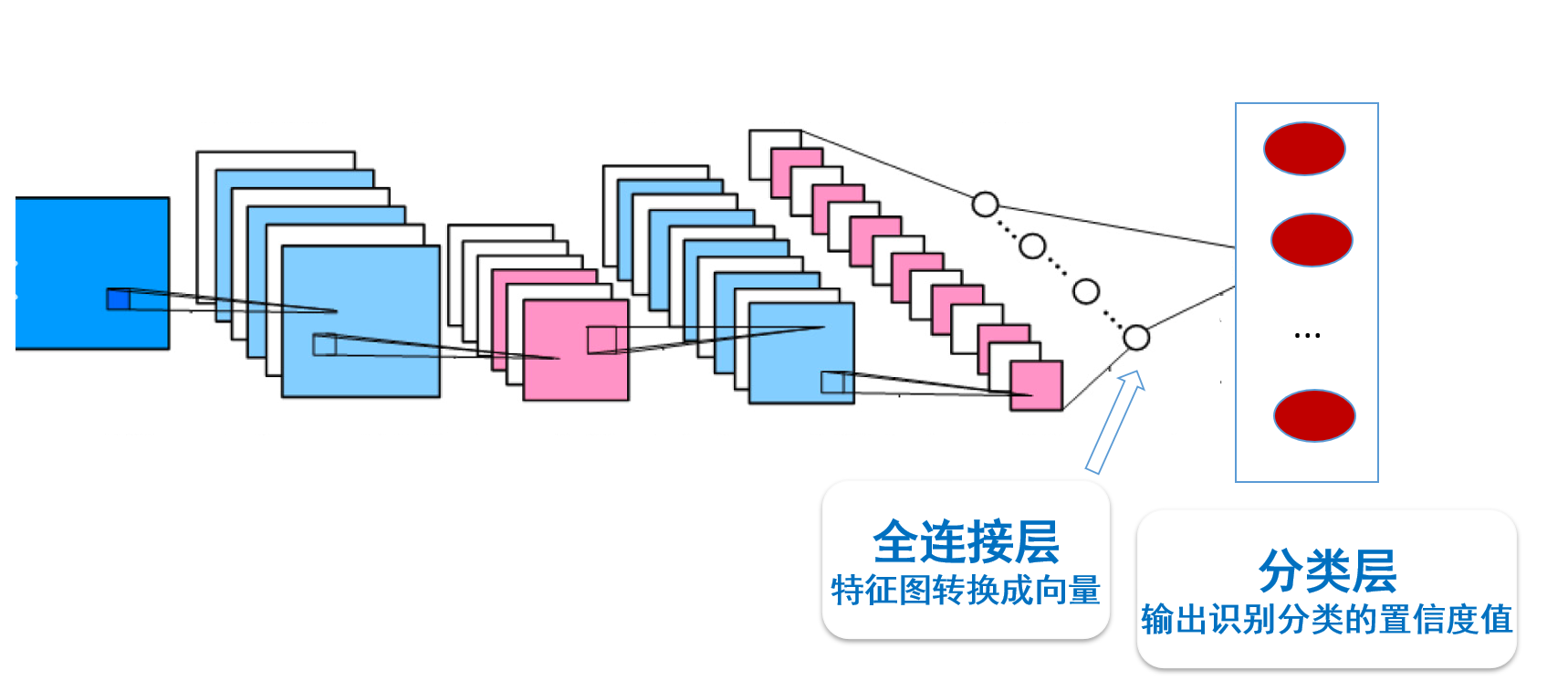
对于输入的海量标注数据，通过多次迭代训练，卷积神经网络在若干次卷积操作、接着对卷积所得结果进行激活函数操作和池化操作下，最后通过全连接层来学习得到输入数据的特征表达，即分布式向量表达()

全连接层：将我们前面的特征图转化为向量
分类层：就是输出我们的识别分类的置信度值

Padding操作

我们通常使用这个方法，将我们的边缘的图层都填充为，这样我们就可以学习到我们边缘的知识了，补充的大小就是根据我们的步长来定，比如说我们原来的图像是，采用的卷积核，然后步长为，这样的话我们想要全部训练，就需要将原先的图像填充为，这样就可以全部训练到了！

神经网络正则化

缓解神经网络在训练过程中出现的过拟合问题，我们采用两个范数去约束他

范数：数学表示为，指模型参数中各个元素的绝对值之和。范数也被称为“稀疏规则算子”（）
范数：数学表示为，指模型参数中各个元素平方和的开方。

范数会趋向于产生少量的特征，而其他的特征都是，而范数会选择更多的特征，这些特征都会接近于

循环神经网络

适合用于处理处理序列数据（如文本句子、视频帧等）

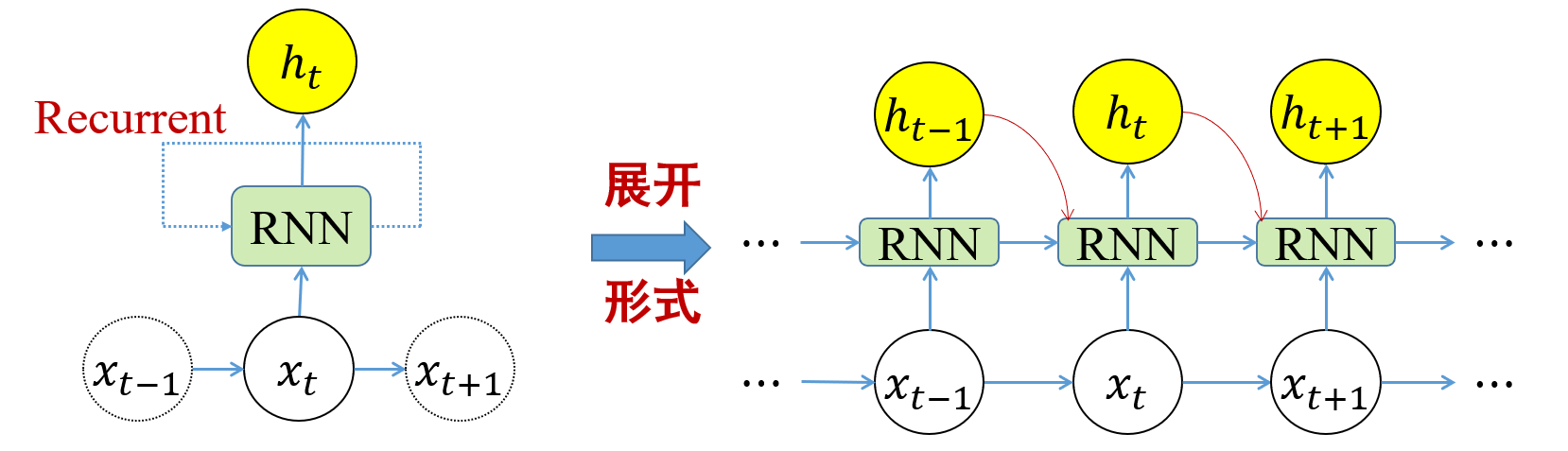
对于序列数据，在时刻循环神经网络单元会读取当前输入数据和前一时刻输入数据所对应的隐式编码结果，一起生成时刻的隐式编码结果。接着将后传

在处理数据过程中，构成了我们的循环体其中，是激活函数，中间的和是我们的模型参数

当前时刻的隐式编码输出不仅仅与当前输入数据相关，与网络已有的“记忆”也有着密不可分的联系

综合起来看，我们有以下的公式： $时刻输入时刻输入时刻输入$

这样我们就完成了神经网络的记忆

可利用反向传播算法和梯度下降算法来训练参数，称为“沿时间反向传播算法()”

由于每个时刻都有一个输出，所以在计算循环神经网络的损失时，通常需要将所有时刻上的损失进行累加

这种训练方式被广泛运用于文本的训练，因为单词之间存在前后依赖，这种依赖会被有效利用起来，得到各自单词的隐式编码以及句子的向量表达

第六章 深度学习

知识点