人工智能导论笔记Chapter7

Posted on | In , |

供南开大学计算机学院和网络空间安全学院期末复习使用

免责声明：本人水平有限，笔记难免有错误，请理性使用，切莫完全相信本笔记的所有内容。

分值分配：课上随堂测试考核(10%)、研讨内容(10%)、实验内容考核(40%)和期末考试(40%)

期末考试：30道选择题（每小题2分）4道简答题（每小题5分）2道解答题（每小题10分）

第七章 强化学习

知识点

强化学习问题定义

强化学习可以学习到最大化收益的模式

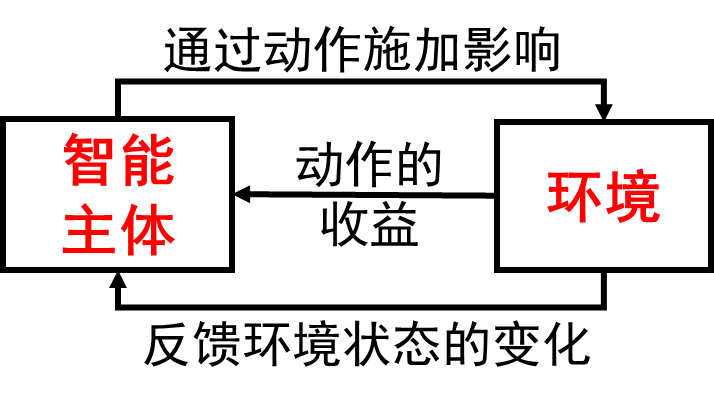
强化学习的一些概念：

智能主体：按照某种策略()，根据当前的状态()选择合适的动作()

  • 状态指的是智能主体对环境的一种解释
  • 动作反映了智能主体对环境主观能动的影响，动作带来的收益称为奖励()

环境：系统中除去智能主体以外的部分，向智能主体反馈状态和奖励，按照一定的规律发生变化

强化学习&监督学习&无监督学习

有监督学习 无监督学习 强化学习
学习依据 基于监督信息 基于对数据结构的假设 基于评价()
数据来源 一次性给定 一次性给定 在交互中产生
决策过程 单步() 无 序列()
学习目标 样本到语义标签的映射 同一类数据的分布模式 选择能够获取最大收益的状态到动作的映射

为了介绍接下来的内容，我们基于一个简单的例子来介绍相关的定义。

在一个的网格中，假设有一个机器人位于，试图从这一初始位置向这一目标位置移动，假设机器人每一步只能向上或向右移动一个方格，到达目标位置则会获得奖励且游戏终止，机器人在移动过程中如果越出方格则会被惩罚，并且游戏终止。那么，如何学习一种策略能够帮助机器人从走到？

在这个问题中，智能主体为迷宫机器人，环境是的网格，状态是机器人当前所处的方格，状态的取值范围为，其中表示机器人出界的情况。机器人每次可采取的行动为向上或者向右移动一个方格，机器人所获得的奖励包括他到达时的正奖励，以及越界时得到的负奖励（惩罚），到达其他状态时不被奖励也不被惩罚。

在这个例子中，我们可以采取随机过程机器人与环境之间的交互。

一个随机过程是一列随时间变化的随机变量。当时间是离散量时，一个随机过程可以表示为，这里的每一个都是一个随机过程，这被称为离散随机过程。我们可以将这个问题视为一个马尔可夫性的离散随机过程，即满足 可以理解成时刻的状态只与时刻的状态有关。

定义离散马尔可夫过程，由于其满足马尔可夫性，因此可以定义状态转移概率。

我们将到达时的奖励定为，出界时的惩罚值为，其他情况下奖励值为。为了比较不同奖励机制的优劣，在每个时刻定义回报来反映该时刻可以得到的累加奖励： 其中折扣因子，表示时刻获得的奖励。

于是，我们得到了马尔可夫奖励过程，其形式化的定义为。这个模型虽然能够用奖励和回报来刻画智能体的目标，但是仍然不能体现机器人的能动性，缺乏让机器人与环境进行交互的手段。

我们引入动作集合，在这个问题中上，右，状态转移概率与动作有关因此将状态转移概率重新定义为 ．奖励也有可能受到动作的影响，因此修改奖励函数为．现在就可以通过来刻画马尔可夫决策过程。

马尔可夫过程中产生的状态序列称为轨迹，轨迹的长度可以是无限的，也可以是有终止状态的。有终止状态的问题叫做分段的，否则叫做持续的。分段问题中，一个从初始状态到终止状态的完整轨迹称为一个片段或回合。

接下来我们对强化问题下定义。首先定义如下函数

  • 价值函数，其中，即在第步状态为时，按照策略行动后在未来所获得的反馈值的数学期望
  • 动作-价值函数，其中表示在第步状态为时，按照策略采取动作后，在未来所获得的反馈值的期望

至此，强化学习转化为一个策略问题：寻找一个最优策略，对任意使得值最大。

最后我们介绍贝尔曼方程，也称动态规划方程。

  • 价值函数的贝尔曼方程

  • 动作-价值函数的贝尔曼方程

价值函数的贝尔曼方程描述了当前状态价值函数和其后续状态价值函数之间的关系，即当前状态价值函数等于瞬时奖励的期望加上后续状态的(折扣)价值函数的期望。而动作-价值函数的贝尔曼方程描述了当前动作-价值函数和其后续动作-价值函数之间的关系，即当前状态下的动作-价值函数等于瞬时奖励的期望加上后续状态的(折扣)动作-价值函数的期望。

基于价值的强化学习

策略优化定理：给定任意状态，如果两个策略和满足如下条件： 那么对于任意状态，有 即策略不比策略差。

下面介绍在状态集合有限前提下三种常见的策略评估方法，它们分别是基于动态规划的方法、基于蒙特卡洛采样的方法和时序差分法。

  • 基于动态规划的方法：使用迭代的方法求解贝尔曼方程组

    缺点：

    • 智能主体需要实现知道状态转移概率
    • 无法处理状态集合大小无线的情况

  • 蒙特卡洛采样：选择不同的起始状态，按照当前策略采样若干轨迹，记他们的集合为，枚举。计算D中s每次出现时对应的反馈，

    优点：

    • 不必知道状态转移概率
    • 容易扩展到无限状态集合的问题中

    缺点：

    • 状态集合比较大时，一个状态在轨迹可能非常稀疏，不利于估计期望
    • 在实际问题中，最终反馈需要在终止状态才能知晓，导致反馈周期较长

  • 时序差分法：通过采样和来估计的取值，并以作为权重接受新的估计值，即把价值函数更新为

学习算法：一种基于时序差分的算法。分为以下几个步骤：

  1. 初始化为初始状态
  2. 比较动作-价值函数最优的动作，设为
  3. 执行动作，观察奖励和下一个状态
  4. 更新
  5. 更新状态，重复执行步骤到，直到是终止状态（一个片段）
  6. 重复执行步骤到，直到收敛

这样的学习算法也会收敛到非最优策略，因为他选择下一步策略总是选择目前已知最优的策略（称为利用），缺乏探索性。

贪心策略：以的概率执行最优的下一步动作，以的概率随机选择下一步动作。

注意这时采样时策略为贪心策略，但是更新是里面计算采用的依然是策略最优的操作。像这样更新时的目标策略与采样策略不同的方法，叫做离策略方法。

将函数参数化，用一个非线性回归模型来拟合函数，例如（深度）神经网络，这使得算法称为深度学习，优点如下

  • 能够用有限的参数刻画无限的状态
  • 由于回归函数的连续性，没有探索过的状态也可通过周围的状态来估计