供南开大学计算机学院和网络空间安全学院期末复习使用

免责声明：本人水平有限，笔记难免有错误，请理性使用，切莫完全相信本笔记的所有内容。

分值分配：课上随堂测试考核(10%)、研讨内容(10%)、实验内容考核(40%)和期末考试(40%)

期末考试：30道选择题（每小题2分）4道简答题（每小题5分）2道解答题（每小题10分）

第二章逻辑与推理

知识点

命题

命题：确定真值的陈述句，无法判断正误的句子都不能作为命题

北京是中国的首都：是真命题

请出去：不是命题，是祈使句

您去开会吗？：不是命题，是疑问句

能被整除：是假命题

这座山真高啊！：不是命题，是感叹句

我正在说谎：不是命题，是悖论

原子命题：指的是不包含其他命题作为其组成部分的命题，又叫做简单命题

简单命题通过联结，形成复合命题

复合命题：指的是包含其他命题作为其组成部分的命题

五种常见的联结词：

命题连接符号	表示形式	意义
与()		命题合取(), 即“p且q”
或()		命题析取(), 即“p或q”
非（）		命题否定(), 即“非p”
条件()		命题蕴含(), 即“如果p则q”
双向条件 ()		命题双向蕴含(), 即“p当且仅当q”

对应的真值表：

真值表

注意：当时，代表的意思是，如果是真的，那么是真的，相当于就是说是的子集，所以如果p为假，那么q一定成立

逻辑

逻辑等价：如果和都具有相同的结果，那么这两个命题就等价

一些常见的逻辑等价
(的交互律)	(蕴涵消除)
(的交互律)	(双向消除)
(的结合律)	()
(的结合律)	()
(双重否定)	(对的分配律)
(逆否命题)	(对的分配律)

蕴涵消除：为假、则命题恒为真；为真、则须为真，所以

推理规则

命题逻辑中常用的推理规则：

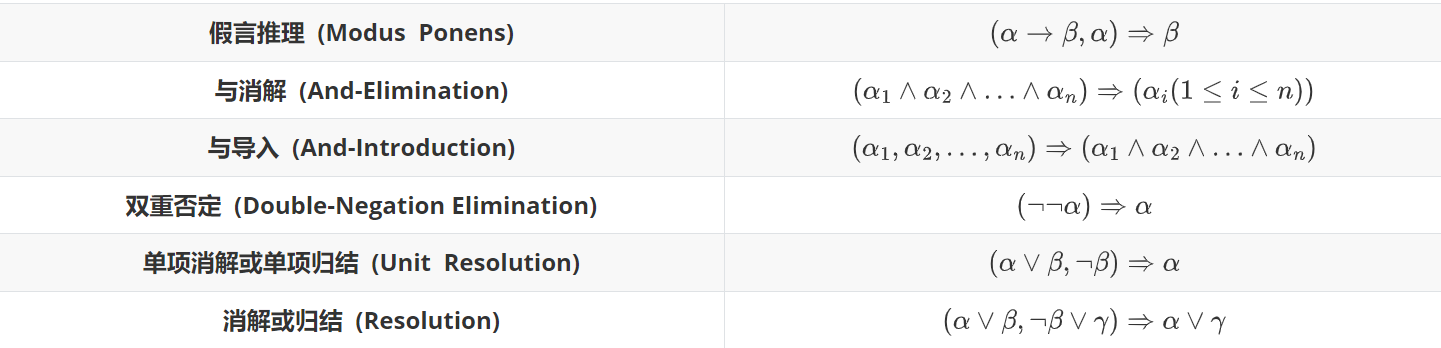
e.g

已知，证明命题是成立的

证明：

通过蕴涵消除得到

通过消解与归结得到

再和前面的做归结运算得到命题正确

重点看一下书本上的例题2.3，例题2.4和例题2.5

范式

范式：

析取范式：有限个简单合取式构成的析取式
合取范式：有限个简单析取式构成的合取式

假设为简单的合取式，则为析取范式

假设为简单的析取式，则为合取范式

析取范式与合取范式统称为范式

一个析取范式是不成立的，当且仅当它的每个简单合取式都不成立

一个合取范式是成立的，当且仅当它的每个简单析取式都是成立的

任一命题公式都存在着与之等值的析取范式与合取范式，且命题公式的析取范式和合取范式都不是唯一的

问题：求的析取范式与合取范式

(析取范式)

(合取范式)

谓词逻辑

谓词逻辑：引入更强大的逻辑表示方式，分离其主语（个体和群体）和谓语（关系），这就是谓词逻辑

个体：指的是在所研究的领域中可以独立存在的具体或者抽象的概念

谓词：用来刻画个体属性或者描述个体之间的关系存在性的元素，其值为真或者为假

函数与谓词的区别：

函数中，个体变量用个体变量代入后，还是个体
谓词中，个体变量用个体变量代入后，就变成了命题，结果是或者是

量词

量词：

全称量词：全称量词用符号表示，表示一切的、凡是的、所有的、每一个等。表示定义域中的所有个体，表示定义域中的所有个体具有性质
存在量词：存在量词用符号表示，表示存在、有一个、某些等。表示定义域中存在一个或若干个个体，表示定义域中存在一个个体或若干个体具有性质

全称量词&存在量词：

$∀𝑥¬𝑃(𝑥)≡¬∃𝑥𝑃(𝑥)$ $¬∀𝑥𝑃(𝑥)≡∃𝑥¬𝑃(𝑥)$ $∀𝑥𝑃(𝑥)≡¬∃𝑥¬𝑃(𝑥)$ $∃𝑥𝑃(𝑥)≡ ¬∀𝑥¬𝑃(𝑥)$

合式公式：

命题常项、命题变项、原子谓词都是合式公式

如果和是合式公式，那么都是合式公式
如果是合式公式，是个体变元，则和也是合式公式

谓词逻辑的推理：

全称量词消去:
全称量词引入:
存在量词消去:
存在量词引入:

已知：

试证明：

使用全称量词的消去与引入就可以证明了
$(∀𝑥)(𝑃(𝑥)→𝑄(𝑥))\\ 𝑃(𝑥)→𝑄(𝑥)(消去全称量词)\\ (∀𝑥)(𝑄(𝑥)→𝑅(𝑥))\\ 𝑄(𝑥)→𝑅(𝑥)(消去全称量词)\\ 𝑃(𝑥)→𝑅(𝑥)(假言三段论)\\ (∀𝑥)(𝑃(𝑥)→𝑅(𝑥))(引入𝑥)$
看课本30页例题2.11和例题2.12

自然语言的形式化

就是将我们人类使用的自然语言，用谓词逻辑表示出来，就可以进行推理了

例题2.13和例题2.14

已知:
请证明：

(7 , 10消解)

知识图谱推理

知识图谱可视为包含多种关系的图

可将知识图谱中任意两个相连节点及其连接边表示成一个三元组（）

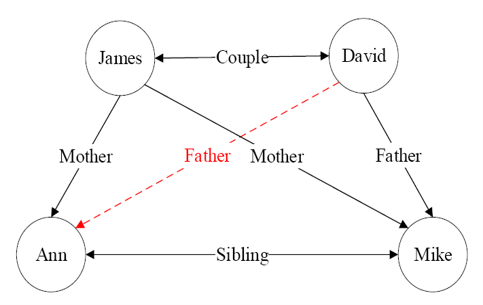
比如说的意思就是，前者是后者的爸爸，中间的表示两者之间的关系，图中的红色的线需要通过推理才能得到

知识图谱推理就是通过机器学习等方法对知识图谱所蕴含关系进行挖掘

如何对知识图谱中的关系进行推理？一共是两种方法

1.归纳逻辑程序设计 ( $，$ )算法

作为的代表性方法， $（）$ 通过序贯覆盖实现规则推理。

推理手段：

推理思路：从一般到特殊，逐步给目标谓词添加前提约束谓词，直到所构成的推理规则不覆盖任何反例

对目标谓词或前提约束谓词中的变量赋予具体值，如将这一推理规则所包含的目标谓词中和分别赋值为和

那么我们需要添加哪些谓词呢？我们根据中的信息增益值来判断

$FOIL\_Gain=\widehat{m_+}\cdot\left(\log_2\frac{\widehat{m_+}}{\widehat{m_+}+\widehat{m_-}}-\log_2\frac{m_+}{m_++m_-}\right)$

其中，和是增加前提约束谓词后所得新推理规则覆盖的正例和反例的数量，和是原推理规则所覆盖的正例和反例数量

我们依次将谓词加入到推理规则中作为前提约束谓词，并计算所得到新推理规则的增益值。基于计算所得增益值来选择最佳前提约束谓词。

背景知识样例集合	目标谓词训练样例集合

然后就一个一个计算下来，算出增益值最大的那一个前提约束谓词

计算出第一轮加入信息增益最大，然后将其加入前提约束中去，将训练样例中与该推理规则不符的样例去掉

这样一直进行运算，直到最后的推理规则不包含反例就可以了

具体见课本例题2.15

FOIL	FOIL算法
输入	目标谓词，的训练样例（正例集合和反例集合），其他背景知识
输出	推导得到目标谓词的推理规则
1	将目标谓词作为所学习推理规则的结论
2	将其他谓词逐一作为前提约束谓词加入推理规则，计算所得到推理规则的信息增益值，选取最优前提约束谓词以生成新推理规则，并将训练样例集合中与该推理规则不符的样例去掉
3	重复过程，直到所得到的推理规则不覆盖任意反例

2.路径排序算法

就是判断路径关联是否能支持表述两者之间的关系

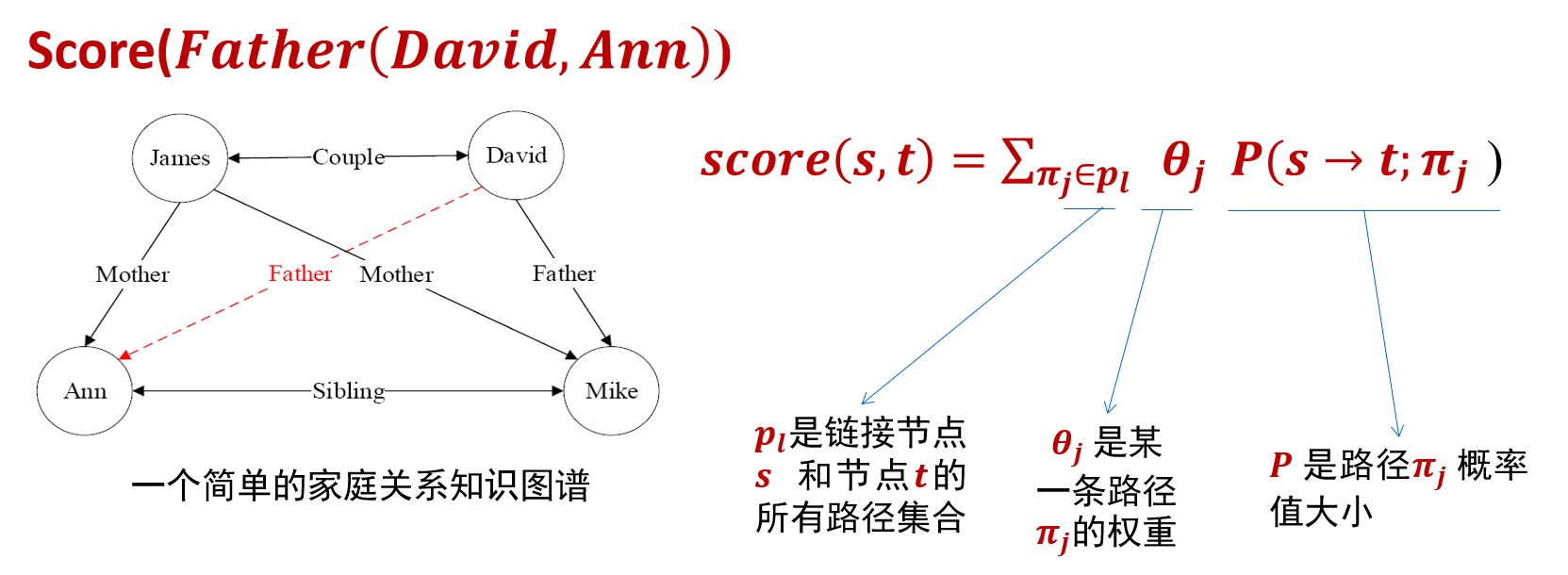
特征抽取：生成并选择路径特征集合。生成路径的方式有随机游走（）、广度优先搜索、深度优先搜索等。
特征计算：计算每个训练样例的特征值。该特征值可以表示从实体节点𝑠出发，通过关系路径到达实体节点𝑡的概率；也可以表示为布尔值，表示实体到实体之间是否存在路径；还可以是实体和实体之间路径出现频次、频率等。
分类器训练：根据训练样例的特征值，为目标关系训练分类器。当训练好分类器后，即可将该分类器用于推理两个实体之间是否存在目标关系。

具体示例看书本例题2.16

因果推理

(辛普森悖论) ：在总体样本中成立的某种关系在分组样本中恰好相反

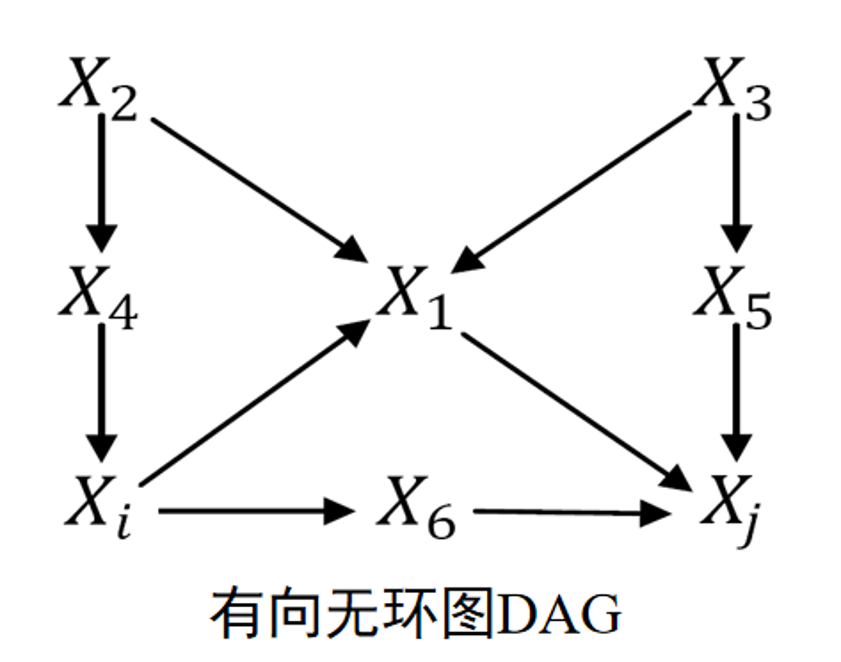
有向无环图（）

(考点)写出以下的联合概率形式，并区分内生变量和外生变量

联合分布为 $│ │ │ │ │$

内生变量是里面的，被其他影响的；外生变量是不由其他元素决定的

D-分离

分离：对于一个图，如果 $、、$ 是三个集合（可以是单独的节点或者是节点的集合），为了判断和是否是条件独立的，在图中考虑所有和之间的路径(不管方向)。对于其中的一条路径，如果满足以下两个条件中的任意一条，则称这条路径是阻塞（）的：路径中存在节点

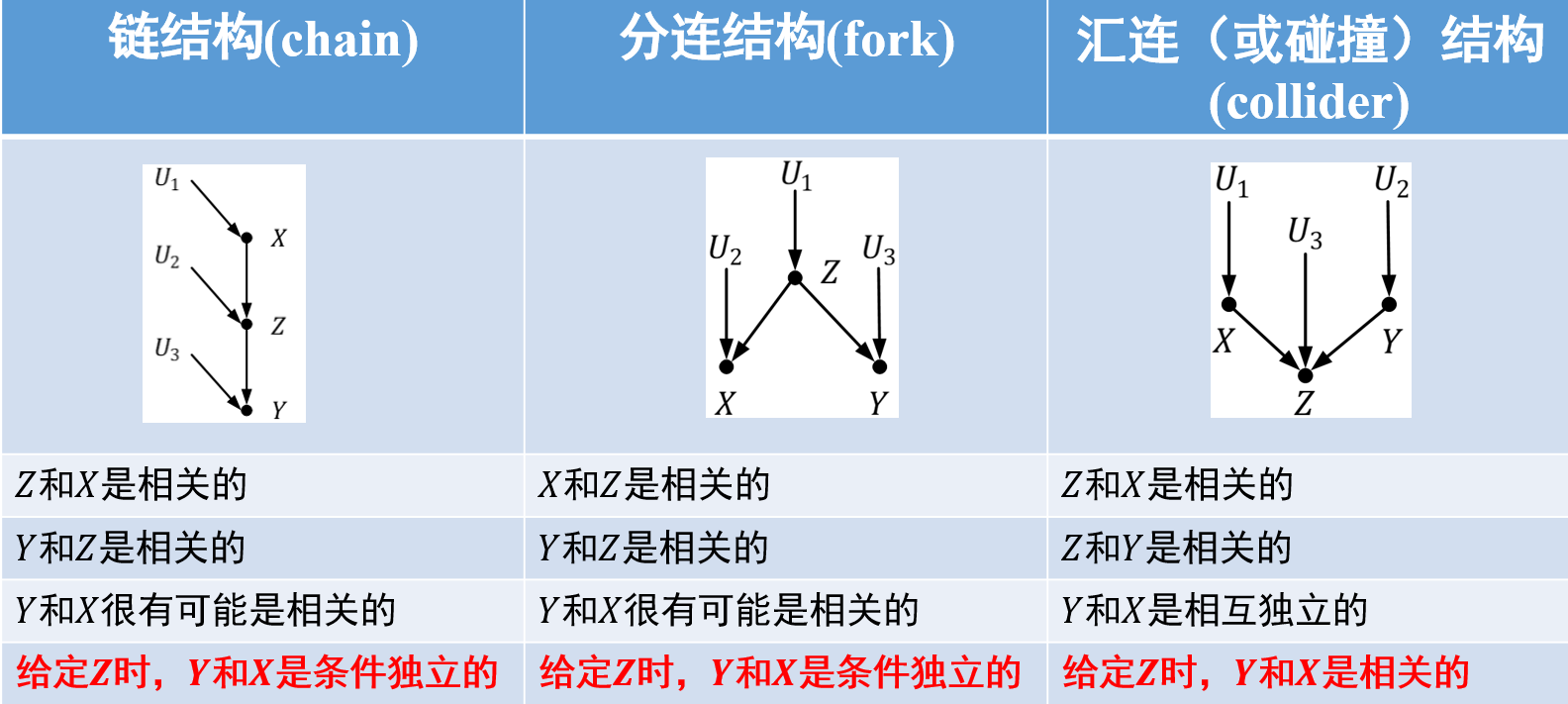
是链结构或分连结构节点, 且
是汇连结构节点，并且或后代不包含在中

如果和之间所有路径都是阻塞的，那么和就是关于条件独立的；否则和不是关于条件独立

上图中到只有一条路径。如果能找到该路径上的任意节点对其进行阻塞，则和是条件独立的。否则不是。

条件为时，只有当汇连节点或者的子节点不包含在条件中的时候，才能阻塞。由于是的子节点，因此不能阻塞。只有当分连接点包含在条件中的时候，才能阻塞。这里的也不能阻塞。因此和在条件下是不独立的。
同上。
条件为时，对分分连结构节点，在条件集合中，因此可以阻塞。独立成立。

推理总结

推理方法	推理方式	说明
归纳推理	如果(为若干取值)，那么	从若干事实出发推理出一般性规律
演绎推理	如果，那么	是的前提、但不是唯一前提，因此是的充分条件。当然，在特殊情况下也可为的充分必要条件
因果推理	因为，所以	是的唯一前提，因此“如果没有，那么没有”也成立。

第二章 逻辑与推理

知识点

命题

逻辑