人工智能导论笔记Chapter5

供南开大学计算机学院和网络空间安全学院期末复习使用

免责声明：本人水平有限，笔记难免有错误，请理性使用，切莫完全相信本笔记的所有内容。

分值分配：课上随堂测试考核(10%)、研讨内容(10%)、实验内容考核(40%)和期末考试(40%)

期末考试：30道选择题（每小题2分）4道简答题（每小题5分）2道解答题（每小题10分）

第五章 无监督学习

知识点

无监督学习，就是不给​的值，只分类，但是我们不知道其具体的语意

监督学习的特征：

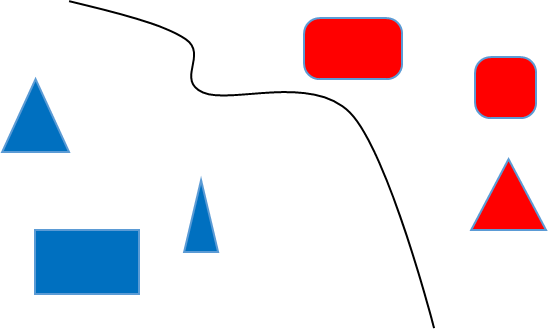
无监督学习的特征：

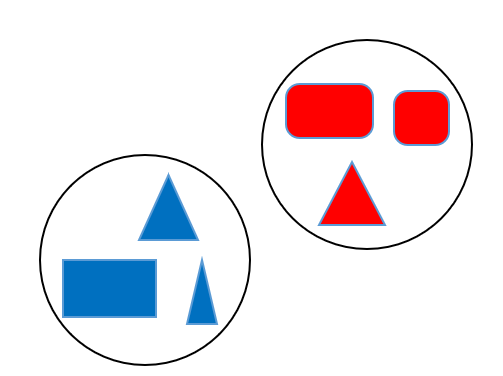
可以看出我们的监督学习是对我们的数据进行了分类，并且能够得知其类别；无监督学习只能起到分类的作用

我们的无监督学习有自己的相似度函数，比如说对上面的六个东西进行分类，我们根据颜色和形状，分类出来的结果是不一样的

K均值聚类(K-Means)

算法原理

输入：个数据，并且没有任何的标注

输出：个聚类结果

我们的目标是，将个维的数据分为个聚簇，使得簇内方差最小化

两个维数据之间的欧氏距离为 我们的欧氏距离越小，就说明我们类内越相似，反之欧氏距离越大就是类内越不相似

K-means聚类算法步骤

1. 初始化聚类质心
   • 初始化个聚类质心，
   • 每个聚类质心所在集合记为
2. 将每个待聚类数据放入唯一一个聚类集合中
   • 计算待聚类数据和质心之间的欧氏距离
   • 将每个放入与之距离最近聚类质心所在聚类集合中，即
3. 根据聚类结果，更新聚类质心
   • 根据每个聚类集合中所包含的数据，更新该聚类集合质心值，即：
4. 算法循环迭代，直到满足条件
   • 循环步骤
   • 终止条件：达到迭代次数上限，或者前后两次迭代中，聚类质心基本保持不变

聚类算法的缺点

• 需要事先确定聚类数目
• 需要初始化聚类中心，而且会对结果产生很大的影响
• 算法是迭代执行，时间开销非常大
• 欧式距离假设数据每个维度之间的重要性是一样的

K均值聚类算法的应用：图像压缩，文本分类等

主成分分析(PCA)

是一种特征降维的方法，我们在过程中会将其化繁为简，降低我们的特征维数

方差

方差等于各个数据与样本均值之差的平方之和之平均数

方差描述了样本数据的波动程度 其中是我们的样本均值

协方差

我们用协方差来衡量两个变量之间的关系

• 当协方差 时，称与正相关
• 当协方差时，称 与负相关
• 当协方差时，称与不相关（线性意义下）

为了归一化处理，我们采用了皮尔逊相关系数来对其进行约束 皮尔逊相关系数的性质如下：

• 越大，线性相关度越大
• 的充要条件是存在常数和，使得
• 表示两者不存在线性相关关系（可能存在其他非线性相关的关系）
• 正线性相关意味着变量增加的情况下，变量也随之增加；负线性相关意味着变量减少的情况下，变量随之增加。

相关性与独立性：

• 如果X和Y的线性不相关，则
• 如果X和Y的彼此独立，则一定，且X和Y不存在任何线性或非线性关系

在降维之中，需要尽可能将数据向方差最大方向进行投影，使得数据所蕴含信息没有丢失，彰显个性

我们需要保证我们投影后，得到的样本方差最大，这样就不会丢失其中的信息

假设我们有个维的样本数据，构成集合

所以我们的集合可以表示成一个的矩阵

我们使用一个映射矩阵

所以我们的给定的样本可以通过映射矩阵进行降维，从维降到了维

我们用拉格朗日来进行求解

目标函数： 约束条件： 拉格朗日函数： 得到结果：

算法描述：

• 输入： 个维样本数据所构成的矩阵，降维后的维数
• 输出：映射矩阵

步骤：

1. 对于每个样本数据进行中心化处理：
2. 计算原始样本数据的协方差矩阵:
3. 对协方差矩阵进行特征值分解，对所得特征根按其值大到小排序
4. 取前个最大特征根所对应特征向量组成映射矩阵
5. 将每个样本数据按照如下方法降维：

特征人脸方法

我们也是使用主成分分析的方法，来进行特征降维

算法步骤：

跟前面的主成分分析是一样的，降维就可以了

将每幅人脸图像转换成列向量，如将一幅的人脸图像转换成的列向量

我们输入的是的列向量构成的矩阵，和我们降维之后的维数

输出是我们中间的映射矩阵

使用个特征人脸的线性组合来表达原始人脸数据

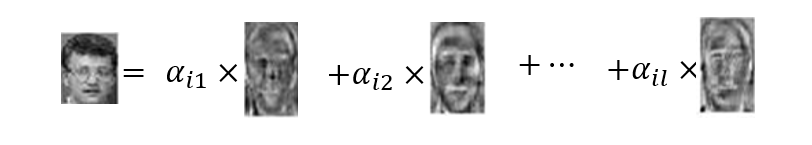
期望最大化算法(EM)

分为两个步骤，第一个是求取期望，第二个是期望最大化

• 在算法的步骤时，先假设模型参数的初始值，估计隐变量取值；
• 在算法的步骤时，基于观测数据、模型参数和隐变量取值一起来最大化“拟合”数据，更新模型参数。
• 基于所更新的模型参数，得到新的隐变量取值（算法的步），然后继续极大化“拟合”数据，更新模型参数（算法的步)。以此类推迭代，直到算法收敛，得到合适的模型参数。

具体例子见：书本页：二硬币投掷例子